3 span continuous indeterminant beam 1

[Crryjy]

Trying to figure out what method to use to calculate the support reaction forces by hand. All 4 supports are FIXED. Each span is 24" and the vertical 700 lb loads are located in the middle of each span. Sorry about the excess beam after the right support, ignore that

 

[electricpete]

You have 4 unknowns (R1, R2, R3, R4).

You need 4 equations to solve based on static equilibrium.

Can you come up with four conditions for static equilibrium involving any forces or moments?

 

[GregLocock]

It's indeterminate, therefore you can't just do forces and moments.

There's lots of ways of solving this, in any Structures 101 book, which way have you tried?



Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[rb1957]

actually if fixed at four supports then this is massively redundant ... 6 redundancies.

or is it trivial ... solve each span in isolation ? if truly fixed at each support, then the beam has zero rotation and zero deflection.
then the LH span is "just" a double cantilever with a single point load ... doubly redundant, but easy to solve. no?
the same solution applies to each span.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[dik]

That's another nice thing about plastic design... it's can be solved directly.

-----*****-----
So strange to see the singularity approaching while the entire planet is rapidly turning into a hellscape. -John Coates

-Dik

 

[rb1957]

2nd thought ('cause I worried about having unequal moments at the supports, if you solved the spans in isolation) ...

solve as a continuous beam over pinned supports (moment distribution)
which will determine the rotation of the beam at each support
and apply an opposing moment to zero out these rotations ...

so 2 redundancies can be solved assuming pinned supports (moment distribution or 3 moment equation)
then the 4 moment redundancies will all interact ... a moment at support 1 will load all 4 supports, and produce rotations of the beam at all 4 supports ...
this means solving a 4x4 matrix to determine the 4 moments.

this method will create the same moment on both sides of each support which sounds a much better solution.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[electricpete]

To me, it seems the conditions of static equilibrium still have to apply even if the beam bends slightly (for accurate moment calculations the displacement just has to be much less than the lever arm distance used to calculate moments, which is 12" or more... so it doesn't seem unreasonable). We assume the applied forces are live forces that remain the same regardless of the deformation. As rb mentioned it's shown as simply supported, so there's no moment created by the supports at their own location.

Let me begin an attempt at what I think would be the solution:

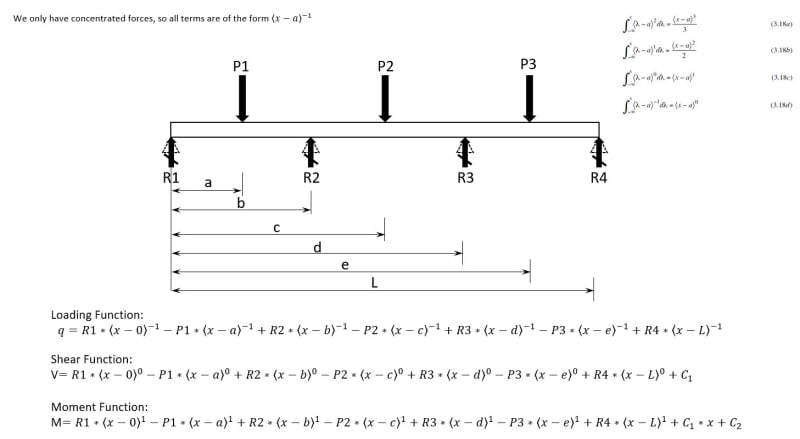
Define positive direction for applied forces F as down and positive direction for reaction forces R1, R2, R3, R4 as up.
Distance between supports is L and force is applied at midspans.

The sum of vertical forces must be zero. Up = Down

R1+R2+R3+R4 = 3*F​

moment about the location of R1: CW = CCW

F*(L/2+3L/2+5L/2) = L*(R2+2*R3+3*R4)​

moment about the location of R2. F spaced at L on each side cancels out. CW = CCW

R1*L +F*3L/2 = R3*L + R4*2L​

moment about the location of R3. F spaced at L on each side cancels out. CW = CCW

R1*2L+R2*L = R4*L + F*3L/2​

moment about the location of R4. CW = CCW

L*(3*R1 + 2*R2+ R3) = F*(5L/2 + 3L/2 + L/2)​

5 equations to solve 4 unknowns. One equation left over to check the solution.

Am I wrong? Or did I say the same thing as whatever rb1957 said? (the only part I recognize is that it's still a 4x4 system to solve)

 

[rb1957]

I think you'll find that taking multiple moment equations collapse, and you're not considering M1, M2, M3, and M4 ... my interpretation of the OP's "fixed" supports. I realise he may mean that the beam is continuous over the supports, and the supports are pinned.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[electricpete]

my interpretation of the OP's "fixed" supports

ok, that's where I went wrong. The figure shows pinned supports. I didn't see the discussion said fixed.

As Rosanne Rosanadana would say... Never mind!

 

[electricpete]

or is it trivial ... solve each span in isolation ? if truly fixed at each support, then the beam has zero rotation and zero deflection.

That makes sense to me fwiw. I don't see any way for the beam to interact on the 2 sides of a truly fixed support, so we solve each side independently.
But if you're not comfortable with that, I'll defer to you on that stuff.

 

[rb1957]

nah, read my later post.

solving it span by span would create different moments on either side of a support, which doesn't sound right.

solving it initially as a continuous beam on pinned will show you how much the beam wants to rotate at each support.
then add moments to cancel these rotations, a 4x4 matrix.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Stress_Eng]

If each support supplies a rigid fixity to the ends of each span and the applied loads are in the middle of each span, then each support on either side of a point load will take 1/2 of the load. The moment seen at the ends of each span will be P/2 x b/4, b being the individual span length.

 

[rb1957]

yes, agreed, if it's that special case.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[GregLocock]

I missed FIXED. They are independent bays, no interaction.

Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[LiftDivergence]

Use Macaulay's method i.e. singularity functions / discontinuity functions.

It is the most robust method for solving statically indeterminate beams by hand.

Everything being discussed will wash out in the loading function of Macaulay's method. You need to know the rules of integration though.

https://en.wikipedia.org/wiki/Singularity_function

Actually, if you are just interested in finding the reactions, and not the shear and moment diagram, you wouldn't have to go through all the integration. Here is an example from Norton. Your's would be more complicated, but you can get the idea/form:

Or if you prefer, basically any other method for continuous beams... moment distribution method / Hardy Cross method, slope-deflection method... virtual work or principle of virtual displacements.

Basically whatever you're comfortable with, most of the time it's taught in second year of undergrad. Check through to your notes to jog your memory.

Keep em' Flying
//Fight Corrosion!

 

[rb1957]

I agree that that is a method, but to show an example of a determinate structure doesn't show how to apply it to an indeterminate one

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[LiftDivergence]

Ok, it's pretty general setting up the loading function whether the beam is determinate or not. It should be something like this:

If you apply boundary conditions at x = 0- and x = L+, that should give enough equations to solve, and C1 and C2 should be zero since the reactions are included in the loading function.

You might also have to keep integrating to get the slope or deflection and apply the BCs to those equations as well.

Here is an example:

https://www.youtube.com/watch?v=zX-A1Jzf-Rg

Keep em' Flying
//Fight Corrosion!

 

[271828]

This is a VERY easy problem using the Force Method, which also is sometimes called the Flexibility Method or Method of Consistent Deformations. Any basic Structural Analysis book would have a section on this method.

There are lots of other methods, but the Force Method would be only about a half page of work, if that. It likely doesn't require any special new knowledge, either.

For this problem:

1. Remove the two interior supports, leaving a 6 ft long simply supported beam with the three point loads.

2. Compute the deflection at the removed supports due to the three point loads.

3. For your 6 ft long beam, compute the reactions that would push the beam back up so there's no deflection at those two interior supports.

 

[rb1957]

OP described the supports as fixed, though I accept he probably meant a continuous beam over pinned supprts.

There are indeed many ways to skin this "cat".

It's bean pointed out that this very special geometry leads to a "trivial" solution.

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.