peteotoole
Civil/Environmental
- Mar 23, 2021
- 4
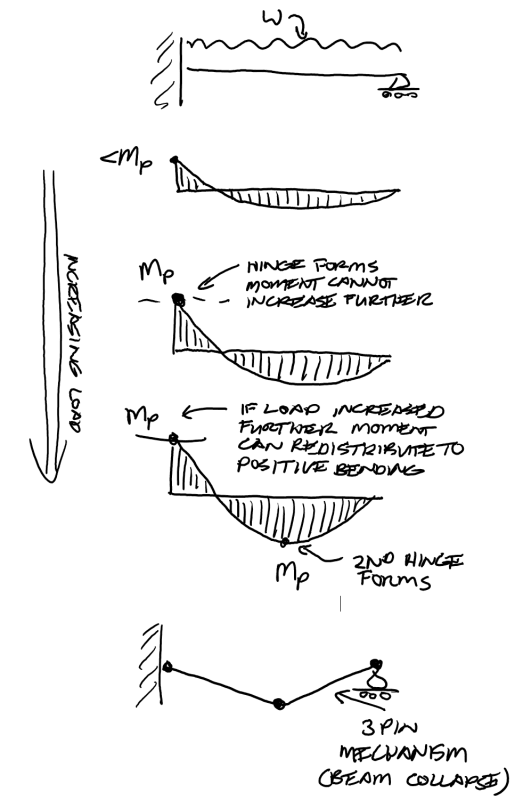
AISC B3.3 doesn't allow you to reduce moments "produced by loading on cantilevers, for design using partially restrained (PR) moment connections, or for design by inelastic analysis...and then further on in the commentary
[/indent]"This adjustment is appropriate only for cases where the inelastic redistribution of moments is possible. For statically determinate spans (e.g., beams that are simply supported at both ends or for cantilevers), redistribution is not possible; therefore, the adjustment is not allowable in these cases. Members with fixed ends or beams continuous over a support can sustain redistribution."
For the picture attached then, would this beam be available for moment reduction because as I read it in the commentary the beam "Must be either fixed at both ends or continuous over a support".

[/indent]"This adjustment is appropriate only for cases where the inelastic redistribution of moments is possible. For statically determinate spans (e.g., beams that are simply supported at both ends or for cantilevers), redistribution is not possible; therefore, the adjustment is not allowable in these cases. Members with fixed ends or beams continuous over a support can sustain redistribution."
For the picture attached then, would this beam be available for moment reduction because as I read it in the commentary the beam "Must be either fixed at both ends or continuous over a support".