I've read this thread (thanks to JStephen):
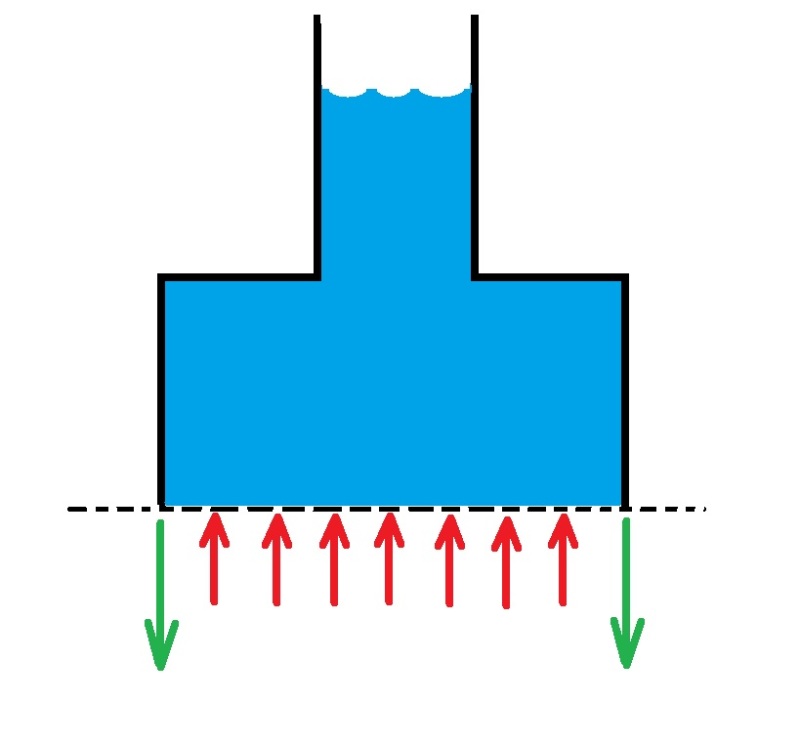
My concern is T1. I understand the concept of an atmospheric cylindrical tank having the static pressure (acting up) equaling the weight/area (acting down) and thus cancelling, which would leave the shell in compression due to the weight of the metal.
My question is about tanks with non-cylindrical geometry. Say we're talking about the same level of consideration (still in a cylinder) but somewhere higher in the tank there's a transition to smaller diameter. Therefore in the equation, the weight term would be less (because less volume of fluid above the level of consideration), and therefore Pstatic and Wf would NOT cancel out, and the net force would be acting up, and T1 comes out positive, indicating tension. I cannot wrap my head around this - I understand the math, but how could the shell be in tension longitudinally?
My concern is T1. I understand the concept of an atmospheric cylindrical tank having the static pressure (acting up) equaling the weight/area (acting down) and thus cancelling, which would leave the shell in compression due to the weight of the metal.
My question is about tanks with non-cylindrical geometry. Say we're talking about the same level of consideration (still in a cylinder) but somewhere higher in the tank there's a transition to smaller diameter. Therefore in the equation, the weight term would be less (because less volume of fluid above the level of consideration), and therefore Pstatic and Wf would NOT cancel out, and the net force would be acting up, and T1 comes out positive, indicating tension. I cannot wrap my head around this - I understand the math, but how could the shell be in tension longitudinally?