Hello,
I just have a question for my understanding on ASME B31.3-2018 Section 319.4(c) Equation 16. I see the limiting factors and the foot note warning, but within the codes itself so this is a more of "the math doesn't seem to add up when I read it - what am I missing?" question?
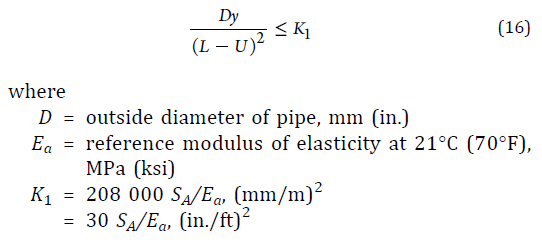

If we look at the terms L and U, for a straight run of pipe these cancel out and the denominator becomes 0. Lets assume its anchored in a straight run of pipe between two pieces of equipment that do not induce thermal expansion, vibrations, etc (say a tank or so). Assume the pipe is straight with no bends or slopes, such that L=U. I can absolutely see applications like this. Obviously at some point the sag and bend will be too much, but the equation does not account for that when L=U.
What am I missing here? Am I misunderstanding a terminology?
I just have a question for my understanding on ASME B31.3-2018 Section 319.4(c) Equation 16. I see the limiting factors and the foot note warning, but within the codes itself so this is a more of "the math doesn't seem to add up when I read it - what am I missing?" question?
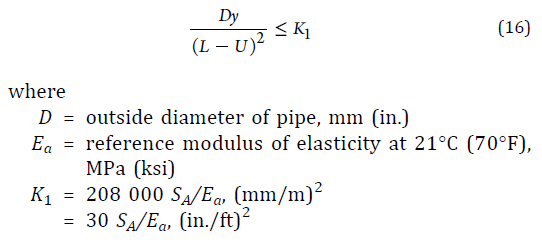

If we look at the terms L and U, for a straight run of pipe these cancel out and the denominator becomes 0. Lets assume its anchored in a straight run of pipe between two pieces of equipment that do not induce thermal expansion, vibrations, etc (say a tank or so). Assume the pipe is straight with no bends or slopes, such that L=U. I can absolutely see applications like this. Obviously at some point the sag and bend will be too much, but the equation does not account for that when L=U.
What am I missing here? Am I misunderstanding a terminology?
