ASME BTH-1 Major Axis Bending

[KB4444]

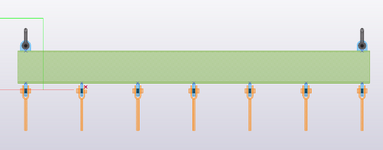
I am designing a 12.25ft lifting beam that is picked up by lifting lugs on the top flange of the beam. The lifting lugs are welded at the ends, being 12ft (144") apart, which I believe means the unbraced length would be 144"? The load is picked up by lifting lugs on the bottom of the beam spaced uniformly apart.

I am trying to size the beam in bending. Using ASME BTH-1: 3-2.3.1 Major Axis Bending of Compact Sections, I am running into a problem with the unbraced length.

I am finding that I do not have a reasonable beam size that is less then Lp (3-7) or Lr (3-10).

Using a W10x33:

Lp = 1.76 x 1.937" x sqrt(29000ksi / 50 ksi)
= 82"
Lr = sqrt(3.19 x 2.136^2 in^2 x 29000ksi x 1 / 50ksi)
[When the bending moment at any point within an unbraced length is larger than that at both end of this length, Cb shall be taken as unity. Therefore, Cb = 1.0]
= 92"

Lu = 144"?

If I am correct with Lu being the space between supports what is my next step? I wouldn't have Lu < Lr, so I believe I am stuck going to an even larger beam size? The bending stress in this situation wouldn't govern.

 

[HTURKAK]

I believe means the unbraced length would be 144"? The load is picked up by lifting lugs on the bottom of the beam spaced uniformly apart.

For your case , Effective length should be LE = 1.2LLT + 2D= 144+2*10= 164 in. ( BS 5950)
Notice that , top and bottom flanges free to rotate on plan.

 

[KB4444]

Is the requirement for needing Lr to be more then Lu (or Le) correct?

Using an extremely heavy W12x106 beam:

Lr = sqrt[3.19 x (3.35^2)in^2 x 29000ksi x 1 / 50ksi]
= 144"

So this would be saying that a W12x106 fails if that is required, which already is a beam size that isn't feasible. For a beam supported on only a 12ft span the bending capacity of this option is grossly overdesigned.

 

[canwesteng]

Use an HSS. HSS are typical for below the hook lifting devices since they cannot buckle laterally (LTB is a prickly thing when there is 0 lateral support, hence the onerous requirements of BTH).

 

[KB4444]

If the plates don't line up from loading to support do you need to worry about wall failure using HSS? Simple solution, appreciate the response, just thinking ahead to my next concern?

 

[BAretired]

The obvious question for me is why not move the lifting lugs 2'-0" inward at each end. Not only do you decrease the unsupported length from 12' to 8', but the maximum moment is reduced by a factor of about 3. With a uniform load over the full length of beam, the negative moment at each lug is w*2^2/2 = 2w. The positive moment is w*8^2/8 - 2w = 6w. With a 12' span, the positive moment is w*12^2/8 = 18w, three times as much. A W10x33 should work with capacity to spare.

 

[canwesteng]

If the plates don't line up from loading to support do you need to worry about wall failure using HSS? Simple solution, appreciate the response, just thinking ahead to my next concern?

Yes, you need to check the walls. I typically slot the plates through the walls of the hss and weld both sides, to avoid a heavier HSS.

 

[dvd]

AISC has a free publication on lifting beams that has been around for a long time which may provide another perspective - https://www.aisc.org/Design-and-Construction-of-Lifting-Beams

 

[KB4444]

BAretired:
I didn't show above the lifting beam but there are (2) existing monorails that are spaced 12' O.C. so this allows a vertical pickup.

canwesteng:
I will see what I can find for the through plate calculations, thanks for the idea on this.

dvd:
I have not seen this publication, I will review it as well. Thanks.

 

[XR250]

Does't the load cause a restoring moment? Wouldn't that help mitigate LTB?
Seems like it is already near its lowest energy state.

 

[hoshang]

[B]HTURKAK[/B] said: For your case , Effective length should be LE = 1.2LLT + 2D= 144+2*10= 164 in. ( BS 5950)​

a typo: it should be read as: 192.8 in.

 

[ANE91]

Does't the load cause a restoring moment? Wouldn't that help mitigate LTB?
Seems like it is already near its lowest energy state.

This is a salient point. The bottom-flange loads act to rotate the beam back to plumb, at least countering the “torsional” piece of the LTB mechanism.

 

[canwesteng]

It can still rotate and roll over to weak side, though less likely

 

[XR250]

It can still rotate and roll over to weak side, though less likely

I don't see how this can happen. Can you explain further?

 

[canwesteng]

Not sure I can. SCI P360 has some discussion on beams with stabilizing load. You could also dump it into FEA and see what the buckled shape looks like

https://www.steelconstruction.info/images/archive/0/0e/20230424132810%21Sci_p360.pdf

 

[ANE91]

I don't see how this can happen. Can you explain further?

It can still happen. It’s like an arm wrestle — which will win: the buckling mechanism or the restoring mechanism?

 

[BAretired]

BAretired:
I didn't show above the lifting beam but there are (2) existing monorails that are spaced 12' O.C. so this allows a vertical pickup.

A vertical pickup is not necessary if the monorails can resist the horizontal component of the lifting force. This would require a minimum vertical separation between the monorails and the lifting beam.

 

[BAretired]

It's not clear how two monorails twelve feet apart can be used if the load to be picked up is not centered under their midpoint. The load will likely be anywhere on the floor, so it is unrealistic to assume a vertical pickup. An overhead crane capable of spanning the entire floor area is a much better pickup device.

 

[KB4444]

The obvious question for me is why not move the lifting lugs 2'-0" inward at each end. Not only do you decrease the unsupported length from 12' to 8', but the maximum moment is reduced by a factor of about 3. With a uniform load over the full length of beam, the negative moment at each lug is w*2^2/2 = 2w. The positive moment is w*8^2/8 - 2w = 6w. With a 12' span, the positive moment is w*12^2/8 = 18w, three times as much. A W10x33 should work with capacity to spare.

Using this revised lifting arrangement I am still getting an issue with the unbraced length posed for the initial problem, Lu > Lr:

Lu = 8'x12"
= 96"

Lr = sqrt[3.19 x (2.14^2)in^2 x 29000ksi x 1 / 50ksi]
= "91.5

Cb = 1 (unity)
rt = 2.14 in^2 (compression flange + 1/3 compression web area)

Due to this I believe the design would need to be increased from a W10x33, even though capacity already is sufficient?

 

[BAretired]

Using this revised lifting arrangement I am still getting an issue with the unbraced length posed for the initial problem, Lu > Lr:

Lu = 8'x12"
= 96"

Lr = sqrt[3.19 x (2.14^2)in^2 x 29000ksi x 1 / 50ksi]
= "91.5

Cb = 1 (unity)
rt = 2.14 in^2 (compression flange + 1/3 compression web area)

Due to this I believe the design would need to be increased from a W10x33, even though capacity already is sufficient?

Your calculation does not agree with the CISC handbook for laterally unsupported members. You are from Canada, right?

So Mr for a W10x33 is 178 kN-m and Lu = 3160mm, which is 124" assuming G40.21 steel with a yield of 350 kN-m.
At 2500mm, A W10x33 is good for the full Mr, so your calculation appears conservative by comparison.

You seem to be deriving your expression from the ASCE standard with which I am not familiar, but it appears to be ultra conservative.

In any case, it appears to me that you cannot rely on a vertical pickup, because the load could be remote from the monorails.