What is the difference between torsion & minor axis bending? 3

[MelBWasHere]

Say I have a wide flange beam in a simple span condition, no lateral support of any kind.
I apply a point load "X" inches away from the beam centerline at the midspan (so an eccentric point load).
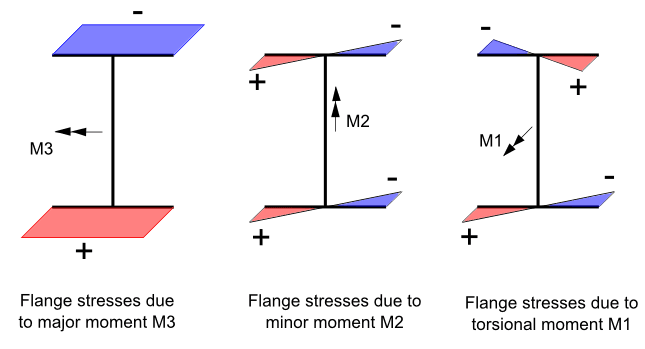
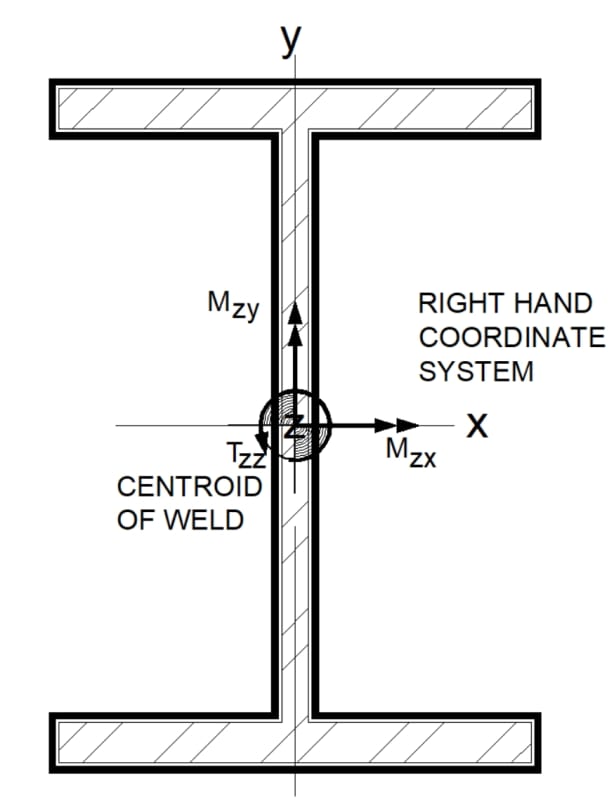
Would this loading condition be considered torsion or minor axis bending? I believe it to be torsion after reading AISC design guide 9 but a friend of mine insists it's minor axis bending.
Which is it? Maybe I'm an idiot & need to go back to school (I will be this fall for my master's, lol), but figured I'd ask here to get more thoughts.

 

[JoshPlumSE]

Both. It applies a torsional force which in open sections is often resolved primarily by minor axis bending. One flange bends in. The other bends out. This is why steel beams generally twist far less in reality than stick models say they will.

Yeah..... Technically, it's just torsion. But, this comment is an excellent example of why the OP posed the original question.

I'll stand by what I said previously (and what KootK said as well). That the torsional warping stresses are best understood through the "equivalent tee" analogy. Since that analogy essentially resolves the torsion into "weak axis bending of the equivalent tee", it is easy to understand why many people think of this as "weak axis bending" behavior. It's not, but that's the shortcut I use to wrap my brain around how these torsional moments are resolved the type of torsional warping stresses they actually produce.

 

[rb1957]

I still dislike calling this secondary bending (so I disagree with "both").

The wiggle-room (or pedanticness) would be that the section reacts torsion by (what appears to be) differential secondary bending about the section axes (which is "really" major bending about the flange local axis). Boy !!?? call a spade a spade

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Tomfh]

To be precise, the applied load is torsion, and there is no minor axis bending.

Yes the applied load is torsional, not an applied minor axis bending load. My original comment about minor axis bending was referring just to the flanges, saying they bend about the beam’s minor axis, in opposing directions, to resolve the torsion. The third image here:

I think we all agree on the mechanics, and are arguing over terminology. I’ll be more careful with my “minor axis” terminology in the future.

It's not, but that's the shortcut I use to wrap my brain around how these torsional moments are resolved the type of torsional warping stresses they actually produce.

I’m not following you here? You’re saying these torsional warping stresses aren’t actually local bending stresses of the flanges/T’s about the beams weak axis?

 

[dik]

As below...

Mzx - major axis
Mzy - minor axis
Mzz or Tzz - torsion

-----*****-----
So strange to see the singularity approaching while the entire planet is rapidly turning into a hellscape. -John Coates

-Dik

 

[JoshPlumSE]

I’m not following you here? You’re saying these torsional warping stresses aren’t actually local bending stresses of the flanges/T’s about the beams weak axis?

You and I are actually pretty much on the same page. But, to be precise, I'm saying that those stresses are simply not weak axis bending stresses on the wide flange. They merely LOOK like weak axis bending stresses. They are actually torsional warping stresses.

Now, if it helps you (or anyone else) to think of this as weak axis bending of the "equivalent tee" then that is what I've been saying all along. That the Equivalent tee analogy simplifies the real torsional warping behavior. It gives us a shortcut to do a quick (and conservative) hand calc on the approximate magnitude of those warping stresses.

That's what I've been explaining to the OP as well. That people (like you) may say "weak axis bending", but that is a misunderstanding. It's really torsional warping stresses.

 

[Tomfh]

They merely LOOK like weak axis bending stresses. They are actually torsional warping stresses.

I’m not sure what you mean when you say these stresses are “actually a torsional warping stress.”

Look at the bottom flange in the “minor” bending case and the “torsion” case. To me, these are the same: a bending force across the flange, bending about the beam’s minor axis.

I understand that in one case these flange forces are part of overall minor axis beam bending, and that in the other case they form part of overall beam torsion, however, in isolation, I thought they were the essentially same? Or are they actually different and just *look* the same?

 

[Stress_Eng]

I read about this form of loading, then identified as differential bending, a long time ago. The document stated, if I remember correctly, that the applied torque would be proportioned out based on the length of the beam governing the relative torsional stiffness of the section and the differential flange bending stiffness.

 

[lexpatrie]

It's torsion due to the eccentricity of the vertical load, it's strong axis bending due to the load directed downward in the strong axis direction. There is no lateral load here that would produce minor axis bending. When you try to turn a door knob, the forces along the plane of the door are zero/minimal.

There's no weak axis bending, (BEYOND the stresses in and out of the plane of the page induced by the torsion - I'm going to speak off the cuff and say that's warping torsion, it adds with the strong axis shear stresses and bending stresses from the vertical load). There is a direct shear flow throughout the entire cross section due to the "direct" torsion, due to twisting, or the twisting results from the induced stresses, you make the call, that's chicken and egg.

 

[rb1957]

"weak axis bending" is a very specific term, and we all know what it means, as distinct to "strong axis bending".

the torsion applied is reacted by a couple in the flanges, putting each flange into "local strong axis bending" (ie bending about the flange's strong axis, which happens to be parallel to the section's weak axis) and together the two flanges are in "differential bending" (as they are bending in the opposite directions).

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[JoshPlumSE]

Or are they actually different and just *look* the same?

In your case you zoomed in only the the bottom flange, in which case the "sense" of the stress is the same. Obviously, if you zoomed in on the top flange the stresses would not have the same direction / sense.

But, they're not the same kind of stress. It's like you're saying that the stress in a flange to to strong axis bending is an axial stress. Yeah, one flange looks like it's in full compression and the other like it's in full tension. That not exactly true. But, it's pretty close. Regardless, it is silly to say that this is axial stress in the flange. It's a bending stress that merely resembles an axial stress in the flange. tress. Same with these warping stresses. They are "warping stresses" that merely resemble weak axis stresses on the flanges of the beam.

I don't think we need to argue about this anymore because it is mostly semantics..... But, this back and forth does likely illuminate why the OP asked the original question. It is the type of discussion that gets confusing if you don't understand what's actually happening.

 

[Just Some Nerd]

the torsion applied is reacted by a couple in the flanges, putting each flange into "local strong axis bending" (ie bending about the flange's strong axis, which happens to be parallel to the section's weak axis) and together the two flanges are in "differential bending" (as they are bending in the opposite directions).

This is my preferred way of outlining it, drawing the distinction between local flange and section weak axis avoids a lot of problems.

----------------------------------------------------------------------

Why yes, I do in fact have no idea what I'm talking about