Raul Villalba
Mechanical
Dear All
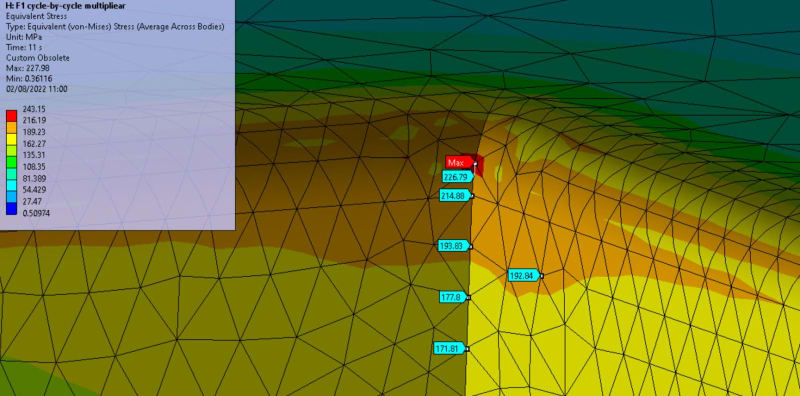
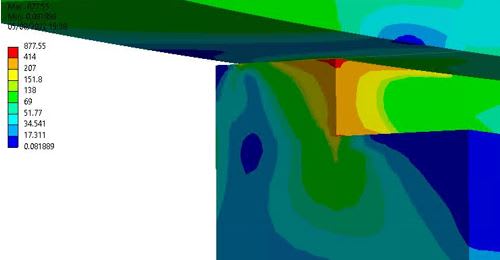
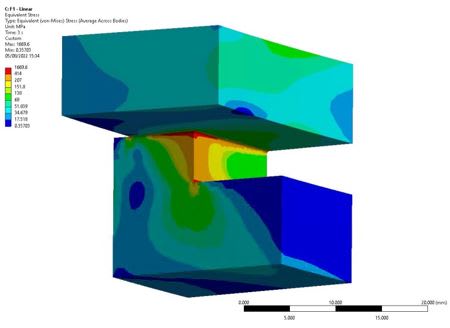
I am assessing a component following ASME VIII-2 Part 5. I have a region (rounded well meshed corner) with high stress concentrations leading to localized plastification. Material model of each verification:
- Plastic collapse: limit load 5.2.3 elastic perfectly plastic bilinear material as specified in 5.2.3.5 step 3.
- Local failure: elastic-plastic 5.3.3. Can I use a elastic perfectly plastic bilinear material instead of a multilinear material since it will lead to more conservative results? The material model in 5.3.3 is not very clear and it just indicates "Elastic-plastic stress analysis" in 5.3.3.1 step 1. In 5.2.4.4 step 3 it allows the use of both: elastic perfectly plastic or material with hardening.
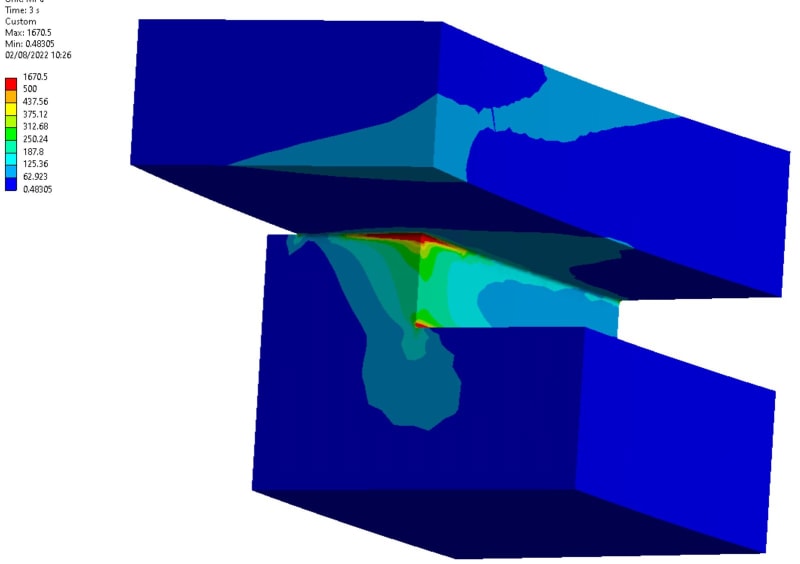
The vessel pressure follows the first load cycle, however the region under analysis is summited to the second load cycle since negative pressure causes a contact opening. Furthermore, unloading may produce a residual compression stress but I do not know yet the hysteresis stress-strain loop.
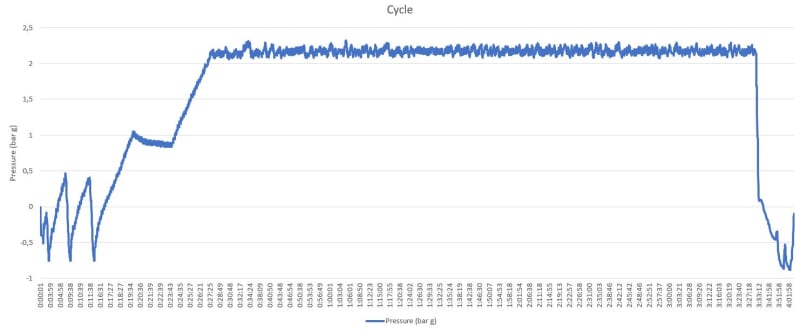
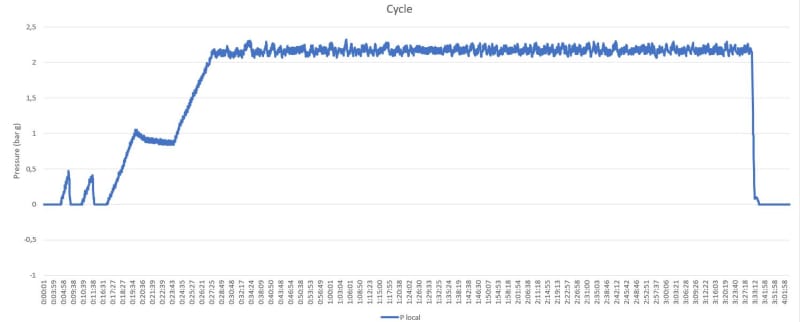
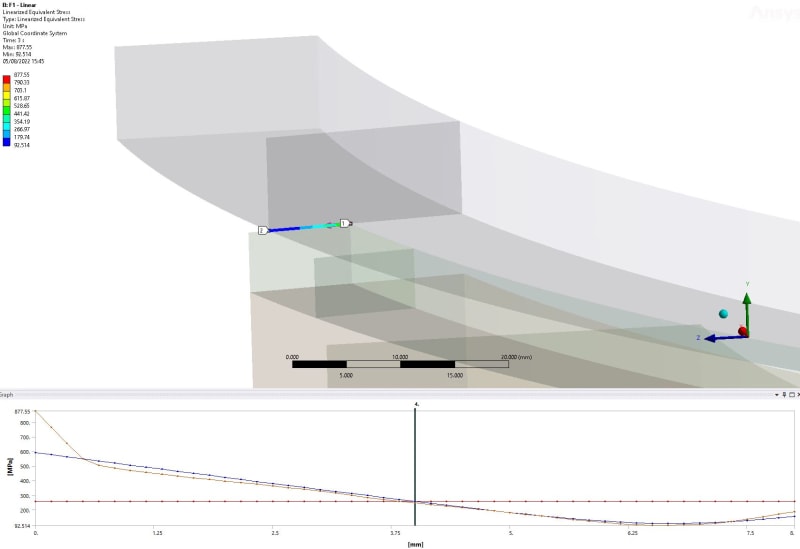
- Fatigue: Elastic-plastic 5.5.4. There are two methods to obtain the effective strain range:
How can I demonstrate that twice yield method can be applied? As far as I know, the two branches of the stress-strain loop needs to be symmetrical.
Can I use a bilinear material instead of a multilinear material (more conservative)? For cycle-by-cycle, is it possible to neglect the kinematic effects if I verify that compressive residual stresses do not exceed compressive plastic yield stress with Bauschinger correction factors?
- Ratcheting: Elastic-Plastic 5.5.7 with bilinear material as specified in 5.5.7.2 step 3.
Thank you in advance.
Warm Regards.
I am assessing a component following ASME VIII-2 Part 5. I have a region (rounded well meshed corner) with high stress concentrations leading to localized plastification. Material model of each verification:
- Plastic collapse: limit load 5.2.3 elastic perfectly plastic bilinear material as specified in 5.2.3.5 step 3.
- Local failure: elastic-plastic 5.3.3. Can I use a elastic perfectly plastic bilinear material instead of a multilinear material since it will lead to more conservative results? The material model in 5.3.3 is not very clear and it just indicates "Elastic-plastic stress analysis" in 5.3.3.1 step 1. In 5.2.4.4 step 3 it allows the use of both: elastic perfectly plastic or material with hardening.
The vessel pressure follows the first load cycle, however the region under analysis is summited to the second load cycle since negative pressure causes a contact opening. Furthermore, unloading may produce a residual compression stress but I do not know yet the hysteresis stress-strain loop.


- Fatigue: Elastic-plastic 5.5.4. There are two methods to obtain the effective strain range:
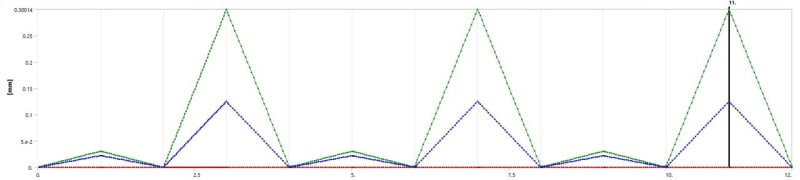
1. Cycle-by-cycle: Kinematic hardening must be included --> I will go for kinematic bilinear hardening material
2. Twice Yield Method: No details --> I will go for an isotropic bilinear perfect plastic material
How can I demonstrate that twice yield method can be applied? As far as I know, the two branches of the stress-strain loop needs to be symmetrical.
Can I use a bilinear material instead of a multilinear material (more conservative)? For cycle-by-cycle, is it possible to neglect the kinematic effects if I verify that compressive residual stresses do not exceed compressive plastic yield stress with Bauschinger correction factors?
- Ratcheting: Elastic-Plastic 5.5.7 with bilinear material as specified in 5.5.7.2 step 3.
Thank you in advance.
Warm Regards.