fem.fan
Mechanical
- Jun 7, 2021
- 33
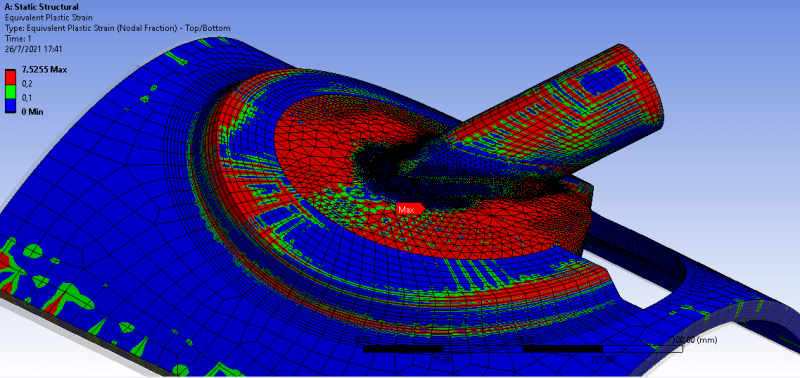
Hi, i am performing an elastoplastic analysis for a vessel nozzle connection according to appendix 46 of ASME XIII Div. 1 using part 5 of ASME XIII div 2.
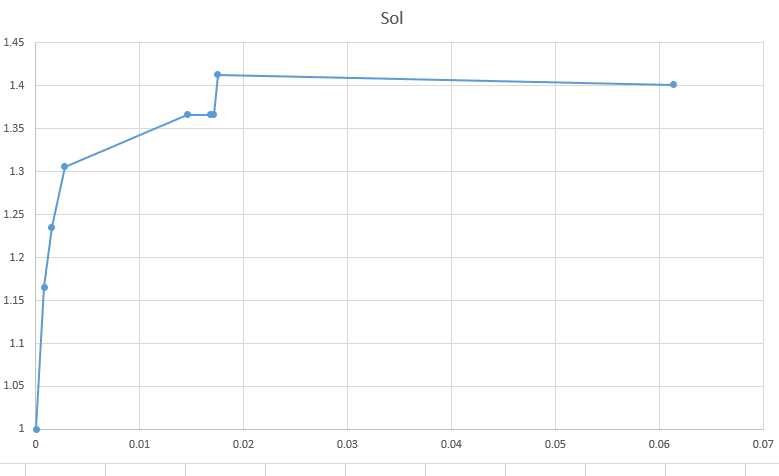
my problem is that when simulation for plastic collapse, i can´t get the plastic strains to converge when refining the mesh.
in other words, i keep refining the mesh and the plastic strains values keep changing. i can´t refine anymore as i run out of RAM (i have 128 GB) and it seems excessive.
i´m using SA 516 Gr 70 Stress strain curve provided by the code
can anyone provide any insight about some criteria used to decide if the results are sufficiently accurate.
this quetion is actually quite genreal as a FEA problem rather than a pressure vessels one.
i ran a very aimple problem of a "beam in cantilever" with a force at the tip using solid elements and i had to produce a highly refined mesh to achieve convergence.
thanks a lot,
my problem is that when simulation for plastic collapse, i can´t get the plastic strains to converge when refining the mesh.
in other words, i keep refining the mesh and the plastic strains values keep changing. i can´t refine anymore as i run out of RAM (i have 128 GB) and it seems excessive.
i´m using SA 516 Gr 70 Stress strain curve provided by the code
can anyone provide any insight about some criteria used to decide if the results are sufficiently accurate.
this quetion is actually quite genreal as a FEA problem rather than a pressure vessels one.
i ran a very aimple problem of a "beam in cantilever" with a force at the tip using solid elements and i had to produce a highly refined mesh to achieve convergence.
thanks a lot,