AMG100
Mechanical
- Nov 29, 2023
- 8
Hi,
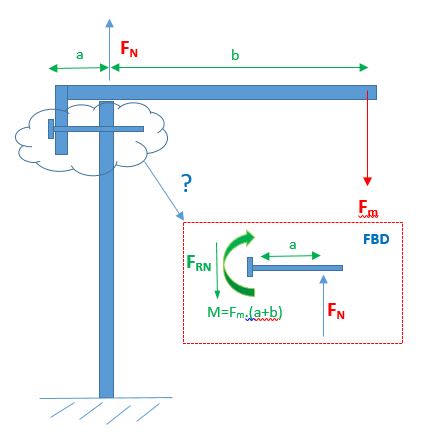
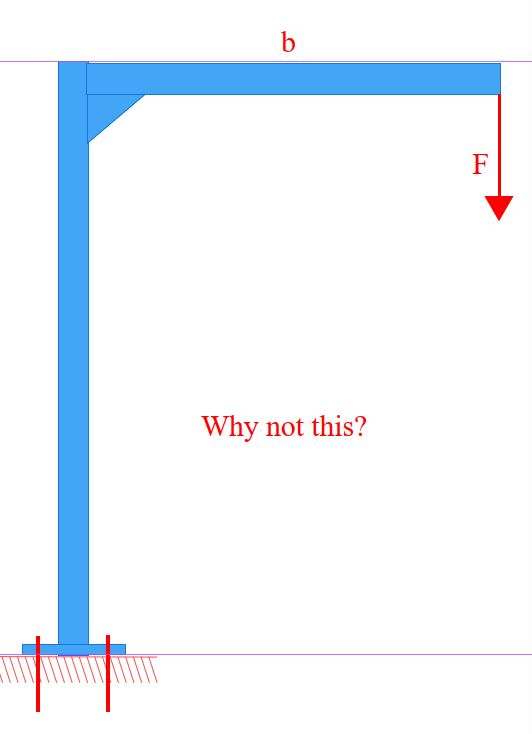
I was hoping somebody may be able to help me generate a FBD for the forces imparted onto bolt/pin located which is designed to prevent rotation of the simple structure shown in the image below
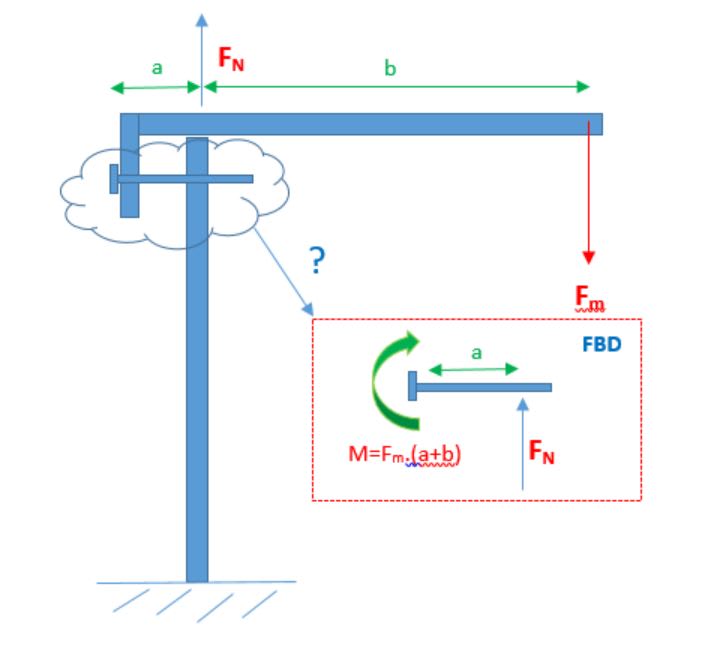
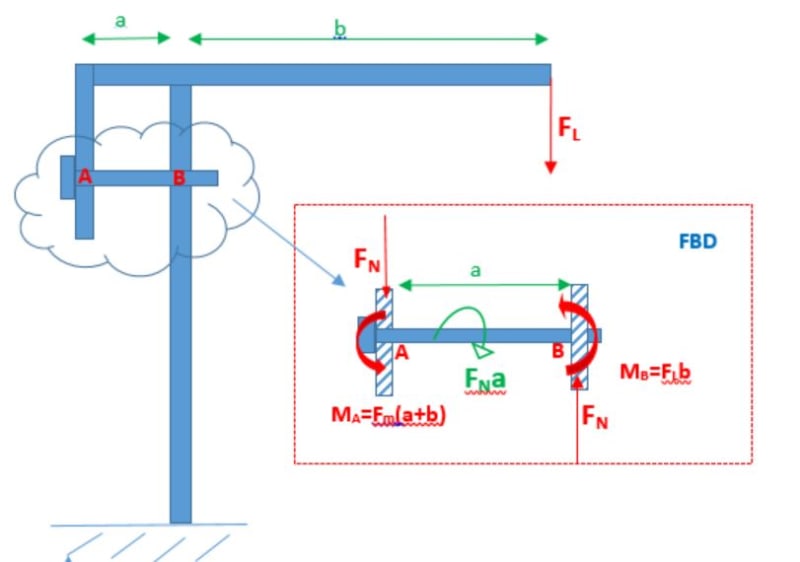
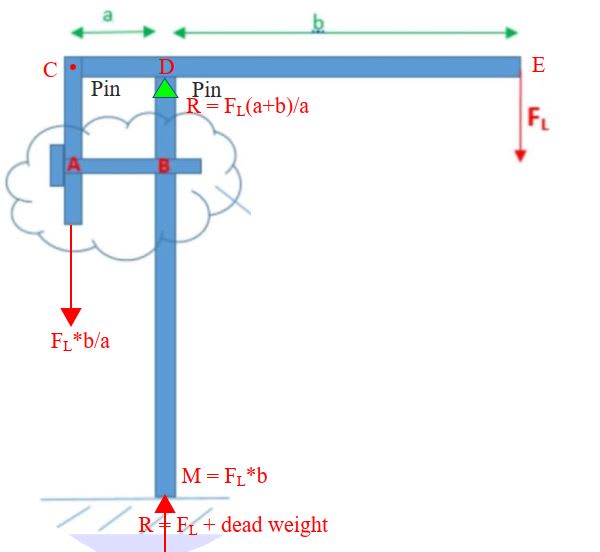
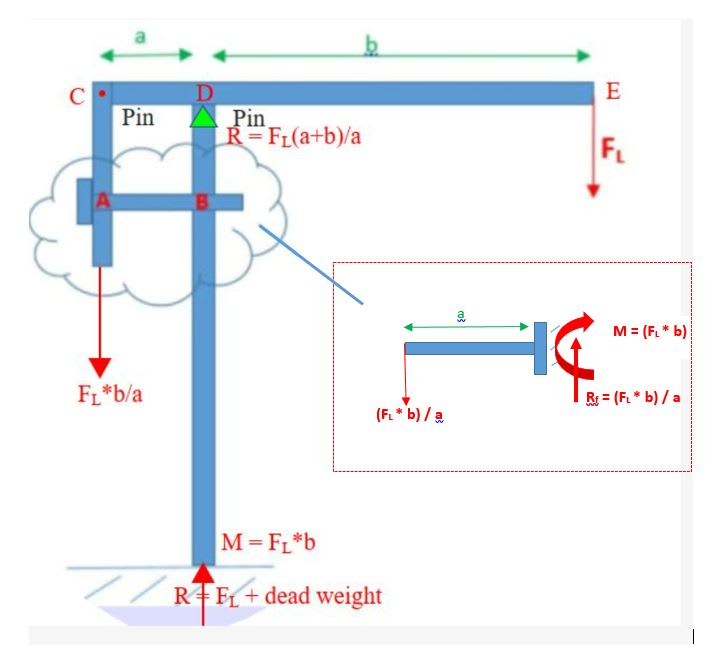
I am assuming that the bolt has moment arm applied at its head (M)due to the applied force (Fm) and the shank has a normal reaction force due to the contact made with the upstand but wanted to check whether these assumptions are correct and the loads appropriately calculated. The plan is to use the FBD to resolve the forces and then determine the bending stress and shear forces on the bolt/pin to make sure it is adequately sized.
If someone who is much more skilled at these things than myself could cast an eye over and advise as to whether I'm on the right track with this, that would be really appreciated.
Thanks in advance,
Anthony.
I was hoping somebody may be able to help me generate a FBD for the forces imparted onto bolt/pin located which is designed to prevent rotation of the simple structure shown in the image below

I am assuming that the bolt has moment arm applied at its head (M)due to the applied force (Fm) and the shank has a normal reaction force due to the contact made with the upstand but wanted to check whether these assumptions are correct and the loads appropriately calculated. The plan is to use the FBD to resolve the forces and then determine the bending stress and shear forces on the bolt/pin to make sure it is adequately sized.
If someone who is much more skilled at these things than myself could cast an eye over and advise as to whether I'm on the right track with this, that would be really appreciated.
Thanks in advance,
Anthony.