ajos6183
Structural
- Sep 18, 2017
- 11
Hi all,
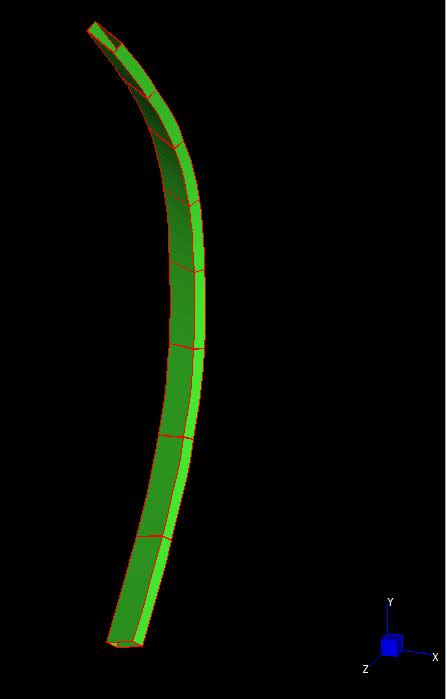
I have been having difficulties working out axial buckling about non-principal axes. I have come up with an example to illustrate my question (please see attached).
Suppose we have a simply supported column under compression only with a midpoint restraint about a non-principal axis. I am interested in finding the first buckling mode in the unrestrained non-principle axis of this column and after that the effective lengths about the principal axis.
Part 1: Finding Pcr
----------------------
My initial thought was that i can use Pcr = pi2 * E * In / L2 where In is the second moment of inertia about the non-principal axis.
For example, suppose that Ix = 42,082,500 mm4 and Iy = 7,382,500 mm4 and the section is rotated 45 degrees, then In = Ix - 0.5 * (Ix - Iy) * (1 - cos(2*45)) = 24,732,500 mm4. I have confirmed this with a simple FE model in Strand7. (Note that subscripts x and y refer to the principle axes whereas n and p refer to the non-principle axes at 45 degrees)
However, this paper seems to say that i cannot do this in the case of a discrete restraint (my situation) and suggests instead an effective or quasi moment of inertia approach. Any thoughts on this?
Part 2: Finding effective lengths about the principal axes
---------------------------------------------------------------------
In this case, i know that Leff,n is the full length of the column and that Leff,p is half the full length. However, i am not sure how to convert these non-principal axes effective lengths to principle axes effective lengths (Leff,x and Leff,y) to be used in design. I look forward to your thoughts and help on this.
Thanks,
Anthony
I have been having difficulties working out axial buckling about non-principal axes. I have come up with an example to illustrate my question (please see attached).
Suppose we have a simply supported column under compression only with a midpoint restraint about a non-principal axis. I am interested in finding the first buckling mode in the unrestrained non-principle axis of this column and after that the effective lengths about the principal axis.
Part 1: Finding Pcr
----------------------
My initial thought was that i can use Pcr = pi2 * E * In / L2 where In is the second moment of inertia about the non-principal axis.
For example, suppose that Ix = 42,082,500 mm4 and Iy = 7,382,500 mm4 and the section is rotated 45 degrees, then In = Ix - 0.5 * (Ix - Iy) * (1 - cos(2*45)) = 24,732,500 mm4. I have confirmed this with a simple FE model in Strand7. (Note that subscripts x and y refer to the principle axes whereas n and p refer to the non-principle axes at 45 degrees)
However, this paper seems to say that i cannot do this in the case of a discrete restraint (my situation) and suggests instead an effective or quasi moment of inertia approach. Any thoughts on this?
Part 2: Finding effective lengths about the principal axes
---------------------------------------------------------------------
In this case, i know that Leff,n is the full length of the column and that Leff,p is half the full length. However, i am not sure how to convert these non-principal axes effective lengths to principle axes effective lengths (Leff,x and Leff,y) to be used in design. I look forward to your thoughts and help on this.
Thanks,
Anthony