bending torsion instability of steel pipe 4

[robyengIT]

Eurocode says that a steel pipe item (part of a structure) is not affected by a bending+torsion instability (i.e. when the torsion stiffness is bigger than the bending stiffness ??). I am looking of literature discussing and explaining such a statement. Thanks

 

[KootK]

In the strictest sense, there is really no such thing as a destabilizing force as a thing considered separately from a destabilizing perturbation (displacement in our context). The destabilizing effect is that of any combination of:

1) A perturbation displacement and;

2) A force which would do positive work when the perturbation is exacerbated.

In this respect:

3) the axial compression load on an Euler column is the "destabilizing load" when a lateral perturbation is considered (external load moves in direction of load).

4) the applied external load in my sketch is the "destabilizing load" when a lateral torsional perturbation is considered (external load moves in direction of load).

5) an axial tension load on a column is a "stabilizing load" when a lateral perturbation is considered (external load does negative work as the ends draw closer together).

An internal force action really cannot be destabilizing, in the strictest sense, precisely because it does no external work. Rather, it is a manifestation of the member strain required to do the external work.

 

[KootK]

Interestingly, by extension of the same logic, this too would be mathematically possible, if practically ridonkulous. No doubt many would consider this to a constitute a point against my reasoning. Presently, I do not.

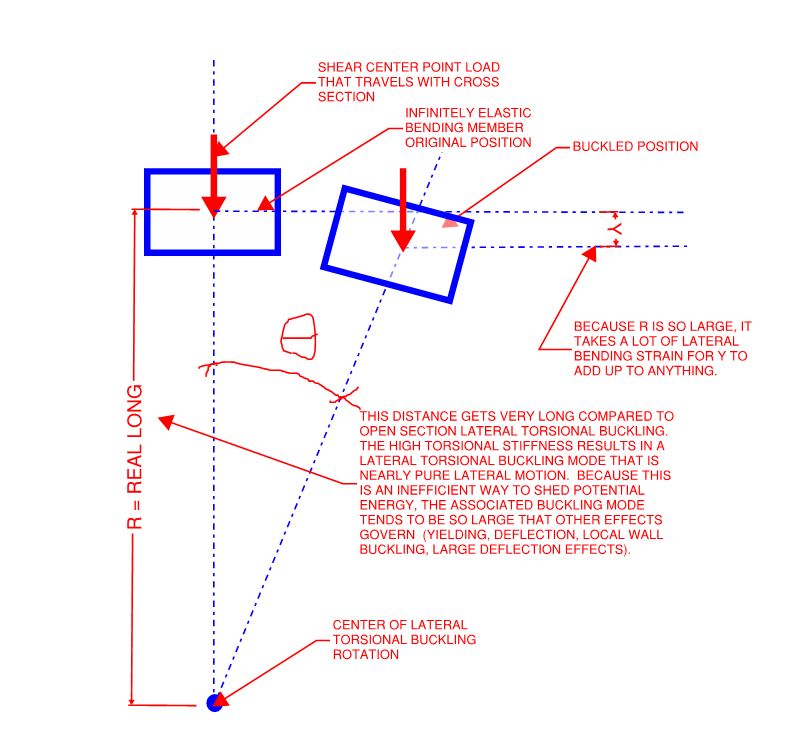
This is somewhat similar to an interesting phenomenon that I noticed when tinkering with buckling analysis using the software package Mastan last fall. If there is any potential for instability, the eigenvalue analysis will find it. It just might be at an applied load ratio (ALR) of 47,000, that's all.

I would play with lateral torsional beam buckling (LTB) and, once all of the expected modes of LTB were restrained, it would start producing "buckling" modes that looked like pure lateral translation (no motion component parallel to the the applied load). They never were pure lateral translation though. Rather, there was always a slight torsional component even if it was imperceptible to the eye.

 

[IDS]

I think it is worth discussing the difference in behaviour in the diagram posted by retired13 on 14 Jan 20 23:31 and those posted by kootk (16 Jan 20 17:15).

If the point load is applied to the top of the pipe then rotation of the pipe will increase the torque and torsional buckling is a possibility, and there will be a well defined theoretical applied load that will cause torsional buckling. If the load is applied exactly at the shear centre rotation does not increase the torque and the theoretical torsional buckling load is infinite.

This applies to a rectangular closed section as well, but in this case the warping effects will make the theoretical torsional/warping load finite.

For a real pipe the load will not be applied exactly at the centre and the section will not be exactly circular with uniform thickness, so there will be a finite torsional buckling load in this case as well, although it likely to be higher than the buckling load due to local wall buckling.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[KootK]

Agreed, that's precisely what I was speaking to below. While non-shear center loading is surely more common in the real world, I thought it most instructive to restrict myself to shear center loading because it eliminates some potentially confusing complexity and makes for an apples to apples comparison to the classical wide flange LTB derivation. That said, I'd be thrilled to discuss the finer points of non-shear center loaded LTB with any interested parties.

4) For any real world tube of such great length, it will likely be prudent to consider the destabilizing effect of loading above the shear center rather than at the shear center. There really are not many common ways to load a tube through the shear center and loads located at other locations may well result in:

a) Pure torsional buckling if it is the case that the tube would stay put and the load source would translate laterally or;

b) Something like constrained axis lateral torsional buckling if it is the case that the load would stay put and the tube were free to translate laterally.

 

[r13]

In my opinion, the load will not always pointing through shear center. As the beam rotates, the load follows but maintain vertical due to gravity (Similar to when floor shakes, we tends to move with it before fall). For the pipe, the additional torsion will produce pure shear in the pipe wall (stable), but for the I beam, due to geometry, it will kick the beam to another state (unstable).

 

[KootK]

That may well be true in practice but it's not how LTB derivations are developed in the literature. Mathematically, I suspect that accounting for that would add a brutal level of complexity.

Nope, your description is in fact both what probably happens in reality AND how the derivations are developed when the load is positioned above the shear center. Mistakenly, I thought that you were describing a situation in which the load did not remain vertical. My bad.

 

[KootK]

For the pipe, the additional torsion will produce pure shear in the pipe wall (stable), but for the I beam, due to geometry, it will kick the beam to another state (unstable).

That I disagree with though. On balance, a pipe will tend to be more torsionally stable than a wide flange. However, stability is not guaranteed by the mere fact that a pipe section is in play. In fact, it would be quite easy to contrive a situation in which an above shear center vertical load would result in torsional instability in a pipe. In many cases that would actually be pure torsional buckling rather than lateral torsional buckling .

 

[IDS]

For the pipe, the additional torsion will produce pure shear in the pipe wall (stable),

The additional torsion will create additional eccentricity, which for small deflections will be proportional to the torsion.

How is that stable?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

that would actually be pure torsional buckling rather than lateral torsional buckling

You are right. That's probably the reason that explains the OP statement:

"Eurocode says that a steel pipe item (part of a structure) is not affected by a bending+torsion instability"

, meaning not to worry LTB for pipes.

 

[KootK]

I'd actually like to see the exact working of that statement, and the prose immediately surrounding it, if anyone has ready access to the document.

 

[IDS]

The torsion is due to a lateral offset between the load and the shear centre, which increases as the pipe twists.

How is that not Lateral Torsional Buckling?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

Kootk I really shouldn't be here at the moment, but you might like to look at:

https://archive.org/details/publicsafetycode?and

[]=eurocode



Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/