TGK07
Student
- Sep 28, 2021
- 2
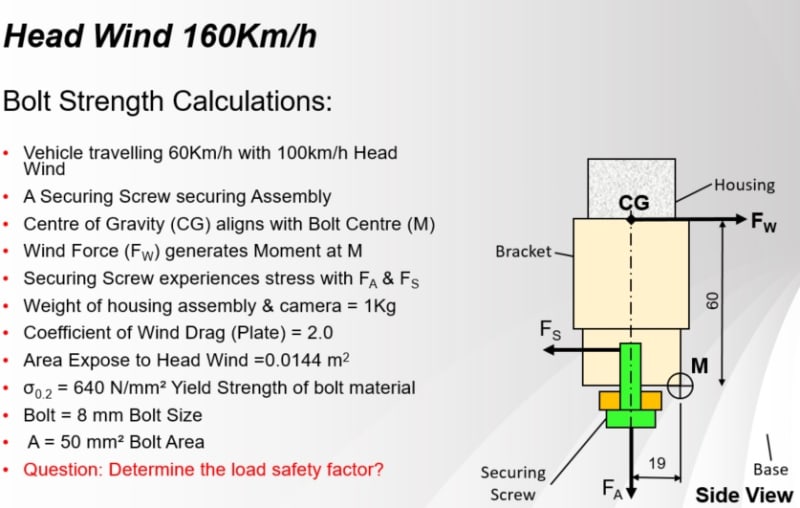

My colleague calculated a safety factor of 1.31. Is my calculation correct?
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
TGK07 said:Point M is the assumed pivot point under headwind when the fastener starts to loosen.

