Michael.Bull
Mechanical
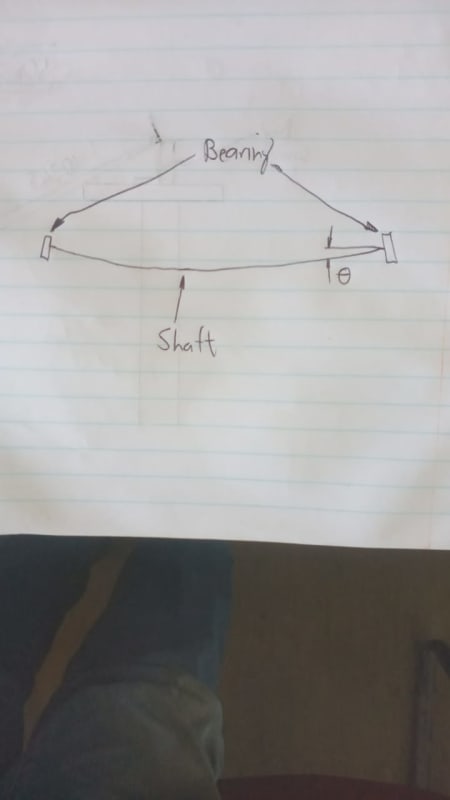
A reel is loaded onto an axle. I want to determine if the tube portion of the axle can support the weight of the reel.
I'm not sure what boundary conditions to apply to the ends. Can someone help me with the boundary conditions?
I'm not sure what boundary conditions to apply to the ends. Can someone help me with the boundary conditions?