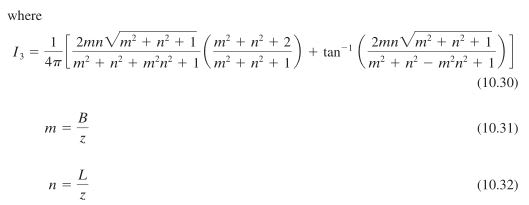canwesteng
Structural
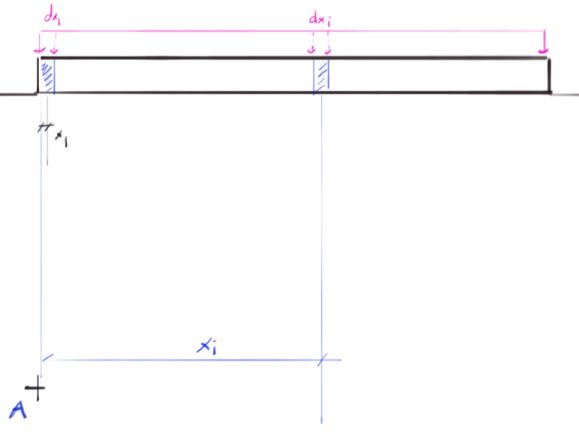
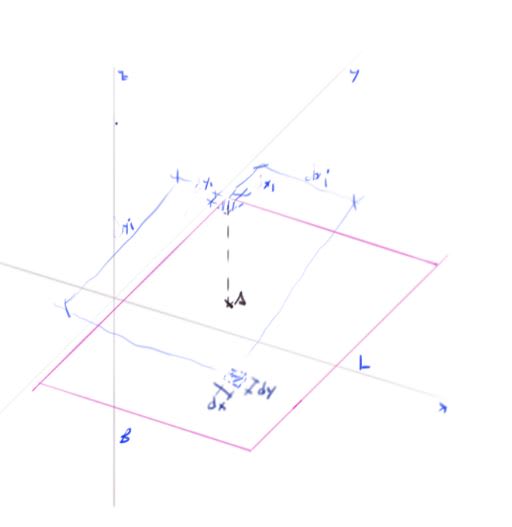
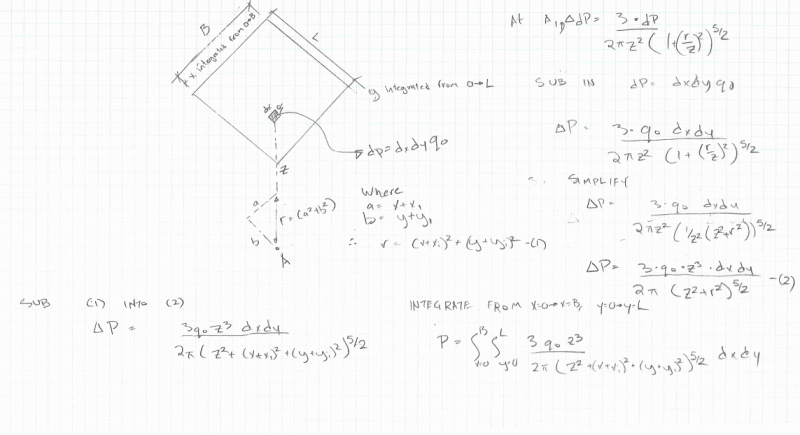
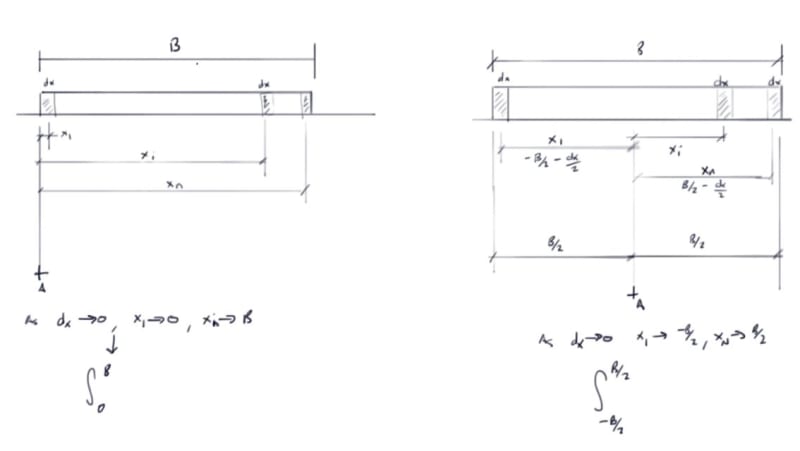
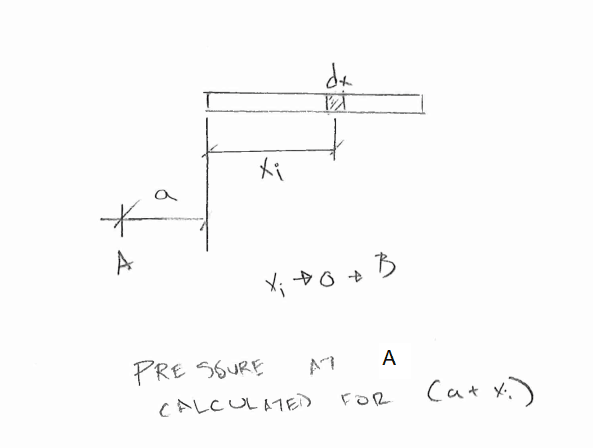
My old college textbooks are giving me a bit of heartburn. I'm looking to program in a function to determine stress below any point for a rectangular foundation, but the way the formula is written, it looks like x/y/z or some combination thereof are variables being integrated in the equation, when in fact I don't believe any variables should be integrated (i.e. it is a constant function being integrated over the base of footing). I think x and y should be cartesian coordinates of the point where stresses are being determined, z is depth below the foundation, and dx/dy are just an infinitesimal square of the foundation to represent a point load. Is this correct? Some snapshots from Das and from my calc below.
Thanks
Thanks