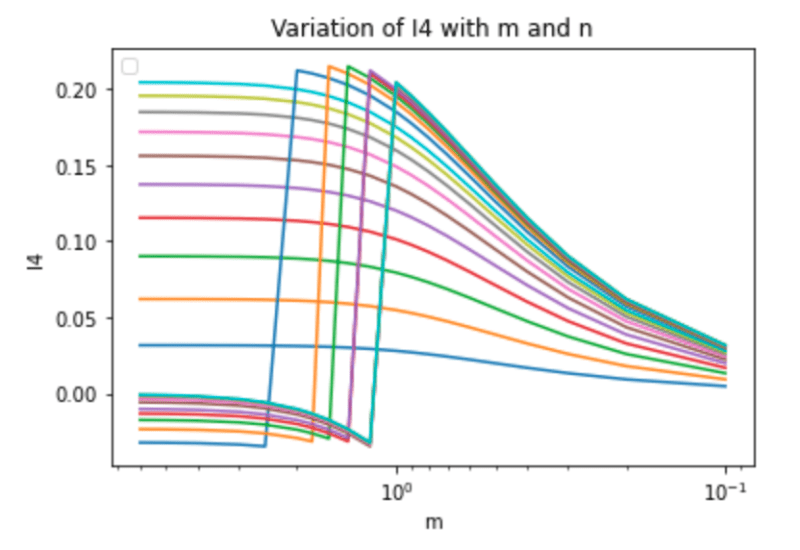
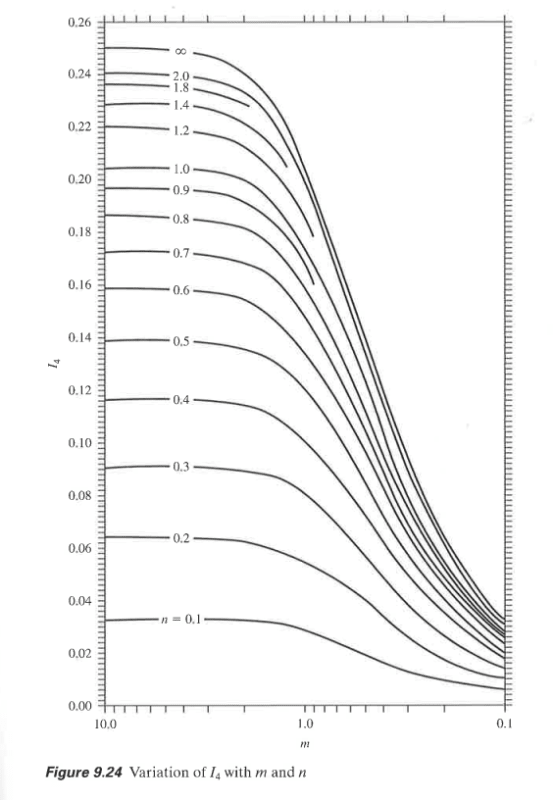
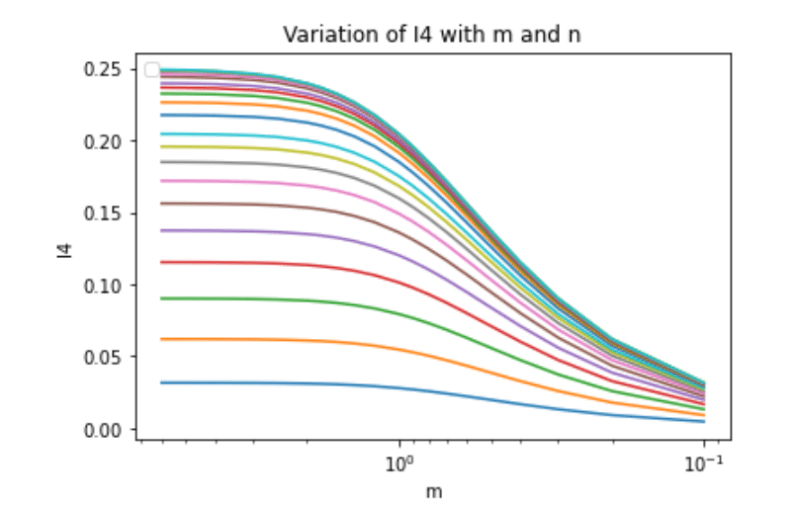
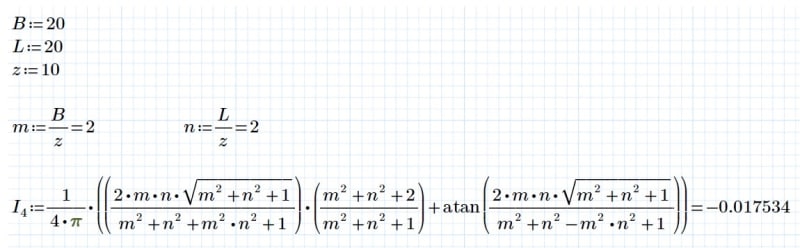Does anyone have a closed form equation for Boussinesq surcharge below corner of a rectangular area? I'm struggling to get the closed form solution provided in Das Equation 9.35 to mach the results on the curves shown in Figure 9.24 for m=2 and n=2. Please see page 3 of the attached pdf reference.
I am trying to program this into a python script and not obtaining correct results, and have checked everything quite a few times so just looking for a sanity check that Das' integration was correct (I'm sure it is). I'm having similar issues with the equation for NAVFAC DM7.1 Figure 2's equations as well for B = 20, L = 20, and z = 10 (i.e. m=2, n=2)
I am calculating an I value of -0.0175 using both Das and NAVFAC 7.1 equations.
Thanks in advance,
I am trying to program this into a python script and not obtaining correct results, and have checked everything quite a few times so just looking for a sanity check that Das' integration was correct (I'm sure it is). I'm having similar issues with the equation for NAVFAC DM7.1 Figure 2's equations as well for B = 20, L = 20, and z = 10 (i.e. m=2, n=2)
I am calculating an I value of -0.0175 using both Das and NAVFAC 7.1 equations.
Thanks in advance,