Buckling Analysis of A-Frame

[Michael.Bull]

I'm trying to determine if the column (column forming the "A") will buckle.

Is my analysis too conservative or not conservative enough?

Assumptions
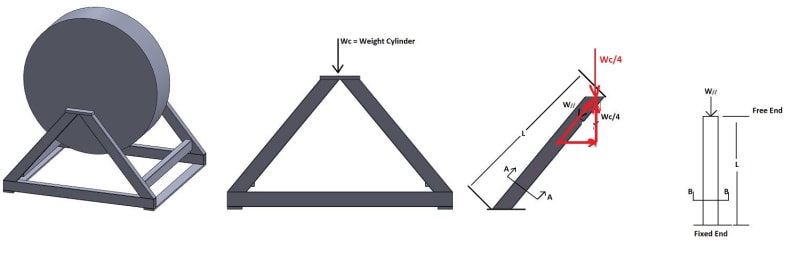
1. Load is being supported by 4 members equally.
2. Section A-A and B-B are the same. Reference picture.

Approach to Solution
1. Calculate The axial force on a member (depicted as W_// in 3rd picture from left)
2. Calculate critical buckling load (right most picture)
3. Compare W_// to critical buckling load. If W_// < critical buckling load, then buckling will not occur.

 

[bugbus]

The critical (elastic / Euler) buckling load will always be an upper bound to the true buckling load, due to the presence of (1) residual stresses, (2) geometric imperfection, and (3) if the buckling occurs as nonlinear buckling, then also due to the effective reduction in stiffness caused by local yielding. There may be one or two other reasons I've forgotten.

In any case, I would not use the elastic buckling load. Check out any steel design code to see how the above effects are accounted for. E.g. AS4100. (There are several others depending on where you live).

I would also consider that the critical strut may carry more than 25% of the total weight, due to misalignment of the cylinder on the frame, the frame not being level, dynamic effects (?), any horizontal effects, etc.

 

[desertfox]

Hi Michael

Your approach seems reasonable to me, the only thing I would say is loading equally on four points won’t happen in practice so I would assume that half the total force goes down the angled section and that ensures a good margin of safety.



“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[rb1957]

is the load is a leg (w/4)/sqrt(2) or (w/2)/sqrt(2) ? I can see your components, but I can see the other (transverse) vector loading the other leg ... so each leg would see double. But then the two legs are not normal, so I'd vector the load/2 over the two leg directions ... yes?? (clear as mud)

This way you have legs in pure compression and no nasty transverse load.

I don't think the top end is free ... at a minimum guided, possibly fixed.

another day in paradise, or is paradise one day closer ?

 

[BAretired]

1. The top end is free if all four members can buckle in the same direction. Looks like they can.
2. The bottom is not fixed unless the cross member is rigidly connected on each side and is infinitely stiff.
3. The load is applied eccentrically to the sloping members, so they will take some bending moment.
4. The isometric view on the left suggests that the sloping members are rectangular in cross section, whereas sections A and B seem to show that they are square.


BA

 

[GregLocock]

Oddly enough my final year project was the failure of truss like systems, in which two of us built half a dozen trusses that would fail in different ways, and compared the actual force vs deflection curves with the theoretical ones. Sadly I can remember no details of the one that scored me all the marks, but it had something to do with the softening of joints as they approach yield and buckling. So the science is known, but it isn't in your basic structures course. Needless to say I have never needed to refer to it again in 40 years.

As a first approximation your sketch looks Ok but I think you would be wise to regard the fixity at the base to be less than encastre.



Cheers

Greg Locock


New here? Try reading these, they might help FAQ731-376

http://eng-tips.com/market.cfm?

 

[human909]

Unless I'm mistaken it seems like you have drawn your vector diagram incorrectly.

Your axial force seems to be less than your Wc/4. And your horizontal reaction vector has a vertical component.

 

[HTURKAK]

May be we can add one more assumption ;
3. The cylindrical weight supported on bearings which provides tie to the top of both A frames. With this assumption , the critical length will be conservatively L..

I should add that , the load calculation W// is not correct.. The two members of frame A apply horizontal thrust to each other.
If top angle of the frame A is 2θ ( pls look to the attached revised sketch )

(W// )* COS θ = Wc/4 ⇒ W// = Wc/(4 *COS θ ) So, one can easily say W// > Wc/4

e.g. the picture implies 2θ = 60 deg. W// = Wc/(4 *COS 30 ) =Wc/(2 √3 )

 

[desertfox]

Hi Michael Bull

I agree with human regarding your vector drawing, my initial thought was to assume the frame was pin jointed and hence the angled leg becomes a two force member and I assume that’s how you were looking at it too.

“Do not worry about your problems with mathematics, I assure you mine are far greater.” Albert Einstein

 

[Michael.Bull]

To HTURKAK & human909
In regards to what you said "W_// > W_c/4"

My line of thinking would say the opposite, that is I believe W_// < W_c/4.

Reason being, I don't understand how a component of a resultant force can be larger than the resultant force.
In my reasoning above, I believe W_// to be the component of W_c/4.

POST EDIT
To HTURKAK & human909
You're right. I just verified with FEA.

 

[rb1957]

I agree with HTURKAK's vectoring. The load applied to one side (two legs) is resolved into two vectors aligned to the legs.

If the leg is fixed at the base, then the leg load vectors are not aligned to the legs (they carry a small transverse shear to create the end moment), but they are mirrors.

another day in paradise, or is paradise one day closer ?

 

[BAretired]

The vector diagram can be shown either way, provided they both end up at the same place. The way the OP showed it, the sloping arrow, W//, represents axial force. The perpendicular arrow represents member shear. It is not wrong to show it that way!!

Edit: Please disregard this comment. Human909's diagram best describes the forces involved. There is a horizontal force between the two sloping members, which I did not consider. Shear may be present from the slight eccentricity of the load, but it will be small and in the opposite direction.

BA

 

[human909]

The vector diagram can be shown either way, provided they both end up at the same place. The way the OP showed it, the sloping arrow, W//, represents axial force. The perpendicular arrow represents member shear. It is not wrong to show it that way!!

True, hence my first comment was elaborated on. You can 'resolve' the gravity vector into a dozen different vectors if you so wish, but it will probably make your life more complicated not less. This should be pretty obvious I'd hope, it is all high school physics.

If you draw it this way for each of the 4 members your secondary vectors don't cancel so there remains unresolved forces. If you sum those forces you get another remaining vector pointing down. Unless you want to repeat the process a dozen times and iterate toward the answer then it is probably best just to take a more sensible approach to resolving your forces.

Reason being, I don't understand how a component of a resultant force can be larger than the resultant force.
In my reasoning above, I believe W// to be the component of Wc/4.

Extremely easily, we have this all the time. Consider the basic problem of a weight hanging in the middle of a rope suspend in two places. You can end up with axial loads several times the applied load.

POST EDIT
To HTURKAK & human909
You're right. I just verified with FEA.

Thanks.

 

[MIStructE_IRE]

I agree with BA in that the top end is free as all members can buckle left or right.

Could you lean them towards each other to get some “eiffelisation”?!