Jack Devlin 1998
Mechanical
- Nov 8, 2019
- 6
Hello,
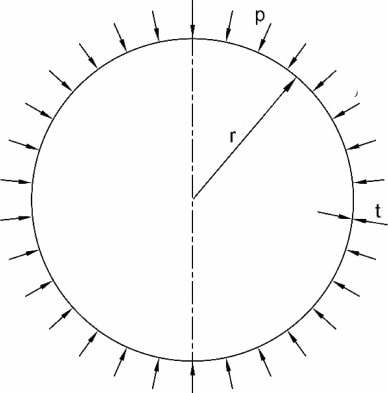
I’m currently carrying out an FEA study looking at the elastic-plastic buckling of externally pressurised cylinders (loaded radially).
In order to verify my analysis, I’d like to compare with analytical equations, however I am struggling to find equations for a cylinder pressurised radially, all I can find are examples of an axially loaded cylinder.
The outer diameter of the pipe is 170mm and the thickness is 10mm.
Thanks in advance for any help.
I’m currently carrying out an FEA study looking at the elastic-plastic buckling of externally pressurised cylinders (loaded radially).
In order to verify my analysis, I’d like to compare with analytical equations, however I am struggling to find equations for a cylinder pressurised radially, all I can find are examples of an axially loaded cylinder.
The outer diameter of the pipe is 170mm and the thickness is 10mm.
Thanks in advance for any help.