novembertango88
Civil/Environmental
- Feb 11, 2020
- 35
Hi all,
Please can you help?
I'm working thru a critiqued past paper of the IStructE exam, see attached. (ref https://www.istructe.org/resources/exam-preparation/critiqued-exam-answer-script-february-2023/)
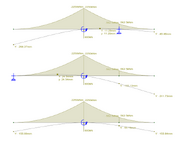
pg 26 shows the calculation of the bracing loads.
The proposed solution for lateral support to the building is by a core of 3No braced bays in each direction (this is to allow for lift/stair access to the core).
The candidate finds the load on each braced bay proportionally but the examiner comments that eccentricity has not been accounted for.
I have tried to account for this by using a beam analogy but am finding that all of the wind load is applied to the central bay.
My working is attached.
Thanks
Please can you help?
I'm working thru a critiqued past paper of the IStructE exam, see attached. (ref https://www.istructe.org/resources/exam-preparation/critiqued-exam-answer-script-february-2023/)
pg 26 shows the calculation of the bracing loads.
The proposed solution for lateral support to the building is by a core of 3No braced bays in each direction (this is to allow for lift/stair access to the core).
The candidate finds the load on each braced bay proportionally but the examiner comments that eccentricity has not been accounted for.
I have tried to account for this by using a beam analogy but am finding that all of the wind load is applied to the central bay.
My working is attached.
Thanks