Question regarding ASME Y14.5-1994 or 2009.
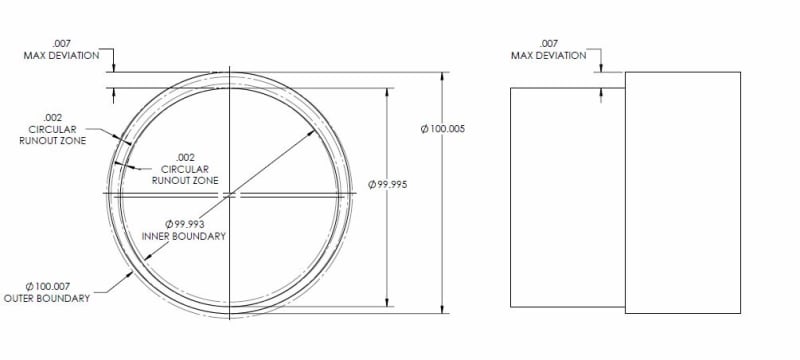
Feature of size 100 ±.005
Circular runout within .002 to a datum axis.
How tall a bump is acceptable in the surface with the runout control?
How would you read and interpret the question: bump size to be measured within the same circular section or from one section to the adjacent one? Am I correct in saying that the answer is .002 if former interpretation is accepted and .010 if the latter one?
Please advise.
Feature of size 100 ±.005
Circular runout within .002 to a datum axis.
How tall a bump is acceptable in the surface with the runout control?
How would you read and interpret the question: bump size to be measured within the same circular section or from one section to the adjacent one? Am I correct in saying that the answer is .002 if former interpretation is accepted and .010 if the latter one?
Please advise.