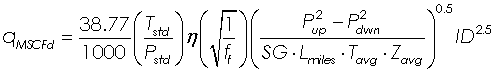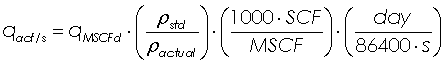Caclulating Head Loss and change in Velocity 1

[phllp581]

After using the Darcy Weishbach equation to calculate head losst through a pipe, can I then take that head loss result and apply Bernoulli equation to calculate the new velocity given the head loss? If I do it this way I seem to get velocity in=velocity out, but this doesn't seem to be right, shouldn't the velocity drop?

 

[katmar]

If the pipe diameters at the inlet and outlet are the same, and if the fluid is incompressible, then the inlet and outlet velocities will be the same. This is a result of the principle of conservation of mass, not a result from Bernoulli.

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[BigInch]

Velocities remain constant with pressure drop, as long as the fluid is not very compressible. Most liquids are not very compressible, so volumetric flow and mass flow both remain constant. Gases change velocity and density with pressure in order to maintain a constant mass flow.

 

[phllp581]

What about when dealing with a gas? How would I go about calculating the velocity out then?

 

[zdas04]

Bernoulli is not a part of this. At all.

I don't recommend using Darcy Weisbach for gases (density changes too much from end to end for an average to be terribly representative), but it can be used if you must. Apparently you are comfortable with finding friction factors using the Moody diagram or the Colebrook equation. For the dP in gas I use the Isothermal Gas Flow Equation

The constants get you to MSCF/day. Notice that the friction factor is Fanning, not Moody (so it is Moody/4). Calculating velocity using standard (i.e., imaginary) pressure and temperature results in an imaginary velocity that is the same everywhere. Not good. I convert to actual cubic feet/s at this point:

Now if you divide the ACF number by pipe area in square feet you get a velocity. The ACF number will be VERY different at the head of the pipe than at the foot of the pipe.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist

 

[phllp581]

What if I wanted to calculate pressure loss through fittings for a gas? I could use the above formula with an equivalent legnth (in-lieu of length), but that only works for some fittings. If I was to run through a restrictor, I would have to use a resistance coeffecient and that would ppush me back to Darcy Weisbach type equation again.

 

[bimr]

What is the application that you are designing?

 

[zdas04]

There is a reason that you can't find equivalent pipe lengths for gas flow--they are too small to be within the accuracy of the equations. I've used the equation above on piping inside of a compressor station and it works fine with small pipe lengths. When I add the fitting lengths that I can look up for Darcy I get the same answer as if I ignore them. The reason for that is that the impact of acceleration effects is so much smaller when your density is 0.06 lbm/ft^3 instead of 62.4 lbm/ft^3. This is the same reason that I don't worry much about erosion in gas streams below about 10,000 psig or below about 0.6 Mach.

If you run through a restrictor, you are lying to yourself if you think that you can just stick in an equivalent pipe length with any equation. I always stop the calc at that point (so that I have a real-ish upstream pressure in front of the restrictor), run the calcs for the restrictor (which can be Bernoulli for something without boundary layer separation like a venturi) and then start the calc again after the restrictor. That is the way that the pipeline models handle it also.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist

 

[phllp581]

My application is trying to determine the pressure loss and velocity change of natural gas that flows through a piping system including several fittings (tees,90s, 45s, restrictors, etc) and valves in an open position. In my problem I know the pressure in, the flow in, and the velocity in to the system. I want to calcluate the pressure drop and velocity across at each fitting to determine where I am losing the most pressure and velocity, so we can make any improvements to reduce/elimante the pressure loss and chagne in velocity. This is for a low pressure system 1.3 psig and 6,135 SFCH of natural gas.

 

[bimr]

Here is a link to an outline on how to size natural gas services.

http://www2.iccsafe.org/states/oreg...dix A_Sizing and Capacities of Gas Piping.pdf

 

[katmar]

The pressure drop of a fluid through straight pipe or through a fitting is proportional to [ρ]v². Velocities for gases are typically around 10x that for liquids, so the v² term increases the pressure drop by about 100, but because your density is roughly 1000th of that for a typical liquid the net effect of [ρ]v² is to decrease typical pressure drops by a factor of around 10.

If you are working with a 3" pipe then 1 m/s water flow will give you a pressure drop of about 0.6 psi/100ft (apologies for mixed units). In the same 3" pipe if you have your gas with a density of about 0.8 kg/m³ and a velocity of 10 m/s then the pressure drop will be about 0.06 psi/100 ft. Again, a factor of 10x less.

So, although it is true that the pressure drop for gases through pipe fittings is generally much less than for liquids it is equally true that generally the pressure drop through the straight pipe is also much less for gases. As it turns out (in my carefully selected example) the pressure drops through straight pipe and through fittings decrease by the same factor when moving from liquids to gases. This makes the minor losses through the fittings, relative to the pressure drop through the pipe, roughly the same for gases and for liquids.

Depending on your application, it may not be realistic to automatically disregard the pressure drop through the fittings for gases. [Start David harassing mode] You could get into bad habits if you do not tackle these problems with the proper rigorous tools every time. [/End David harassing mode]

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[zdas04]

I am not going to get back on that soapbox (although I always keep it close to hand).

In the slide rule days I was a huge fan of all of the shortcuts. Today I do these calcs in MathCad and can iterate a friction factor (for example) until the guess Reynolds Number is within 0.0001% of the resulting Reynolds Number with no effort at all. I can calculate compressibility with a function in a FOR loop without getting a single blister from my slide rule.

With those tools I don't see much upside to using tools developed to give "good enough" answers on a slide rule (which is where the equivalent length paradigm came from). I never use Darcy for gas, or AGA Fully Turbulent (or Panhandle or Wehmouth) any more because today's pipe roughness pushes most problems out of the fully turbulent range of the Moody Diagram.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist

 

[katmar]

The design procedure linked to by bimr looks like it will answer most of your questions. Another very useful reference is the Crane TP410 manual and this will probably fill in any missing information. If you ask areound it is quite likely that one of your colleagues will have one - it is very popular. If you will be doing this type of calculation on an ongoing basis I would recommend buying a copy (Google will find a supplier).

There is one easy observation to make regarding velocities. If your inlet pressure is 1.3 psig then the absolute minimum density you could get to with an outlet directly to atmosphere would be 100 x 14.7 / (14.7 + 1.3) = 92% of your inlet density. Using this and the ratio of the areas of the various pipes it is easy to calculate the maximum velocity attained.

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[zdas04]

Katmar's rho*v^2 term is really key here. With a liquid and a moderate velocity the force trying to straighten a 90° elbow (or the piping off a tee branch) is a measurable impact on the available force (pressure). This application of force is the source of the equivalent pipe length tables. For a gas, velocity is higher, but density is so much lower that the force trying to straighten elbows is diminimus.

On a short system with a lot of elbows and tees I'd include the centerline length of the fittings, but a 3-inch, 3D 90 has a centerline length of around 7 inches. A hundred of them adds 58 ft. On a 1,000 ft system, adding 58 ft would be measurable increase in dP, but just.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist

 

[katmar]

zdas04 has made his reluctance to use the equivalent length method clear, while I am a bit of a fanboy for this method. On most aspects of fluid flow zdas04 and I are usually in agreement but because of our different views on the L/d method I must reply to his last post.

I have to concede that one weakness with the L/d method is that the values given for the equivalent lengths of various fittings vary greatly from source to source and this will lower engineers' confidence in the results. For example, the reference given by bimr above gives an L/d of 8 (my interpolation) for zdas04's 3" 3D bend while the Crane TP410 manual gives it as 12. An important positive that can be taken from this variation is the realization that the calculation of pressure drops through fittings is not an exact science. What little experimental evidence has been published is very scattered and would not show either of these references to be "wrong".

I have tried to pull together what I regard as the best data into a consolidated list of L/d values for a variety of pipe fittings and materials in an article available on line.

Now back to zdas04's example. If the L/d method is used the straight pipe length to be added for each bend would be L/d x d = 12 x 3" = 36". This is significantly more than the 7" centerline length used by zdas04. The total extra length for 100 bends would be 100 x 36 / 12 = 300 ft. Note that the L/d method includes the pressure drop due to wall friction so it is not necessary to add the centerline length to the L/d equivalent length. (Some authors disagree with this statement.) I have never seen a 1,000 ft pipe include 100 off 90 degree bends so this example is an extreme case and the results should not be regarded as typical.

There certainly are examples where the pressure drop through pipe bends and tees can be ignored (such as a gas pipeline) but there are also applications where they must be considered. What makes an engineer different from an automaton is the engineer uses his knowledge and experience to decide what method to apply where.

Katmar Software - AioFlo Pipe Hydraulics

http://katmarsoftware.com

"An undefined problem has an infinite number of solutions"

 

[zdas04]

Katmar,
Let me make my "reluctance" clear. Every source I can find talks about using the equivalent length method for liquid flows. I think the empirical data used in developing the values for pure water are pretty good. When we apply them to non-Newtonian fluids like many crude oils and all emulsions the calculated values are not close to measured data, but with Newtonian liquids they do fine.

I've also never seen them match measured data in equations where the appropriate friction factor was Fanning instead of Moody.

The development of the factors was empirical. I am always reluctant to extrapolate empirical data. If I'm doing a project in water with a SG between about 0.95 and 1.3 I use equivalent lengths without hesitation. I just don't think that the derivations support extrapolation very far outside of that range.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist

 

[georgeverghese]

There is a detailed account on calculating the additional frictional loss for elbows in Perry 6th and 7th editions.

 

[phllp581]

Thank very much for all the help! I was able to use the Isothermal Equation above to get my solution and matched the answer Pipeline Toolbox is giving me for flowing through straight pipe. My next question is how do apply the concept of Resistance Coefficients and Flow Coefficients to this equation? Referencing Crane's I can calculate Resistance Coefficients and Flow Coefficients for the various fittings and valves I am flowing through but need to calculate the pressure drop through these fittings for the natural gas. Crane's refers Resistance Coefficients and Flow Coefficients back to the Darcy-Weisbach equation to calculate the pressure drop, while I would like to continue using the Isothermal Equation (since I am dealing with a gas). Is there a method to convert Resistance Coefficients and Flow Coefficients to equivalent lengths or someother way to go about doing this?

 

[bimr]

There is a chart in this link that converts k factors to equivalent lengths for gas services.

http://www2.iccsafe.org/states/oregon/08_residenti...

 

[zdas04]

bimr,
The link does not seem to work.

Philip581,
If you just MUST do that, then I would calculate a dP using the straight pipe length in the Isothermal equation. Then I would add the factors from Crane to the length and re-calculate the dP with the Isothermal equation. If the difference is tiny then assume the fittings do not matter. If the difference is significant then continue your search.

David Simpson, PE
MuleShoe Engineering

In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual. Galileo Galilei, Italian Physicist