optymista93
Student
Hi,
I'm wondering how You can calculate volumetric flow rate (SCFM=ft2/min) without rotameter installed.
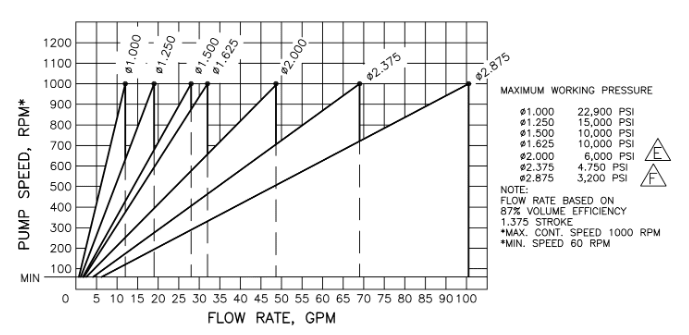
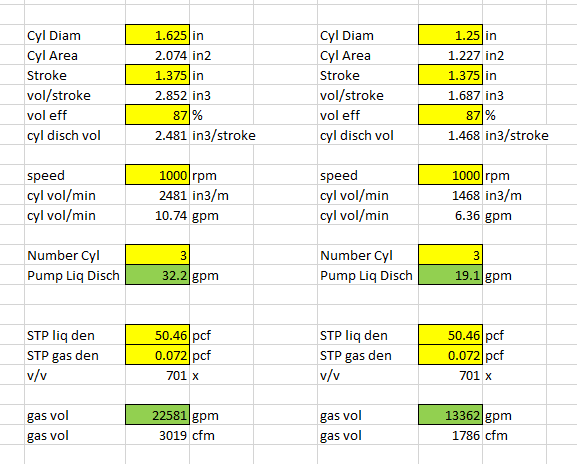
We need to change from 1,625" to 1,25" Cold End. This will change the volumetric flow rate.
Liquid nitrogen is pumped by a hydraulic pump to a vaporizor. How can I calculate gasses volumetric flow rate out of vaporizor?
Thank You in advance!
I'm wondering how You can calculate volumetric flow rate (SCFM=ft2/min) without rotameter installed.
We need to change from 1,625" to 1,25" Cold End. This will change the volumetric flow rate.
Liquid nitrogen is pumped by a hydraulic pump to a vaporizor. How can I calculate gasses volumetric flow rate out of vaporizor?
Thank You in advance!

![[conehead] [conehead] [conehead]](/data/assets/smilies/conehead.gif)

![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif)