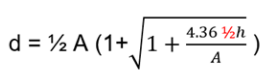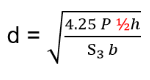Calculation of concrete foundation for steel fence 3

[Damned]

Hello,

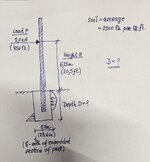
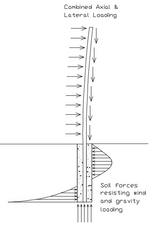
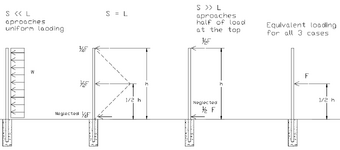
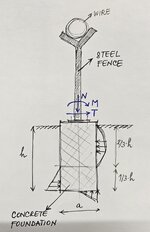
I need to calculate the concrete foundation for the steel fence. I know that these are relatively small foundations/posts and that the dimensions of the foundation of the fence are often adopted according to some guidelines, but I should also attach a calculation that will prove the load-bearing capacity and stability of the foundation and the soil as well. This is neither a classic shallow foundation nor a pile, but belongs to a type of 'deep foundation' whose stresses at the contact of the foundation and the soil looks like this (picture below).



Does anyone have an example of the calculation of this type of foundation, preferably from a standard (ideally European) or a book that I can refer to?

 

[Celt83]

Reference ANSI/ASAE EP486.1 Shallow Post Foundation Design

Behavior is similar to a pile. Note your bottom pressure won't be triangular the moment that would create that distribution is taken out by the lateral resistance through the depth so the base pressure is typically assumed uniform.

 

[dik]

This organisation may be able to help. There could be an update to their manual.

 

[HTURKAK]

​

This subject has been discussed with several threads. Search the forum for steel post foundation. One of them ;​

Design moment of an embedded steel post​

 

[Damned]

Reference ANSI/ASAE EP486.1 Shallow Post Foundation Design

Behavior is similar to a pile. Note your bottom pressure won't be triangular the moment that would create that distribution is taken out by the lateral resistance through the depth so the base pressure is typically assumed uniform.

But is it the same if we have driven/bored column/pile in the ground (picture a) below) and if we have a steel column and 'more vertical' concrete foundation (picture b) below)? And what are the general limits of D/b (depth/width) ratio of the foundation in order to include the lateral soil pressure in the calculation? According to some literature that ratio should be D/b > 5, which seems excessive to me, considering that if the typical foundation of a fence post were calculated as an ordinary shallow foundation/footing (picture c) below), it would not pass the stability and stress criteria.

 

[Damned]

This organisation may be able to help. There could be an update to their manual.

Thank you for this manual. I will have in mind this recommendation if I don't find any calculaton.
First, I'm trying to find an example of a calculation.

In an old literature, I found that the problem of calculating such foundations was dealt with by various people, for example: Kleinogel, Frounlich, Sulzberger, Dorr, Prokofiev, Belzecki, etc. I would like to find at least some example of calculation by one of the methods without it being a very complicated science.

 

[Damned]

​

This subject has been discussed with several threads. Search the forum for steel post foundation. One of them ;​

Design moment of an embedded steel post​

I have already read some of the discussions on the forum. Again I run into problems using their diagrams. For example, if my example of foundations, dimensions and forces are as in the picture below, following their example of using the diagram, I get C (coefficient of post stability) values outside the diagram, as well as the L depth coefficient (second picture below). I'm probably doing something wrong somewhere, but I don't know where.



Maybe this force and its moment are just to small to use this properly, I don't know.

I will definitely look for answers in some more discussions here, thank you.

 

[azcats]

IBC Section 1807.3 has the formulae. 1807.3.2.1

Note that the soil characteristic here is passive pressure - not vertical bearing. I'd expect to see something more like 200 psf/ft. Using that I get 5.78' deep.

https://codes.iccsafe.org/content/C...ils-and-foundations#CABC2022P2_Ch18_Sec1807.3

 

[FenceEng]

IBC footing design is not worded very clearly. I've got about 9 pages explaining the IBC footing design proceedure at https://fencedesign.com/footing-design/

 

[Damned]

IBC footing design is not worded very clearly. I've got about 9 pages explaining the IBC footing design proceedure at https://fencedesign.com/footing-design/
View attachment 4059

Thank you very much for this example!

Can you just one more time explain me this part:
"h = Post height in feet. The actual IBC formula uses h for the force’s application height, but as ASCE 7 uses h for the fence height, the ½ h value is used in the formula below as the post strength tables are based on the force being applied at the mid height of the post. This also keeps the variables consistent."
As someone who calculates according to Eurocode (so I'm not that familiar with IBC and ASCE regulations) why is it more correct here to take the height at which the force of the wind acts according to ASCE 7 (h/2), and not according to IBC (h)?

 

[FenceEng]

IBC is not considering a fence post, just any post resisting any type of load and they happened to use h for the force application height to get the moment that must be resisted by the footing.

For a fence post, applying the force at the mid-height provides the equivalent moment at the base as a distributed load or multiple point loads. ASCE uses "h" for the height of a wall or in this case, a fence, so I put that 1/2 h in the IBC formula to keep the variables consistent across different parts of the design guide.

 

[FenceEng]

I've re-written the text to make the differences clearer between the IBC and the design guide procedures.

 

[Damned]

Thanks for the more detailed explanations, just what does this S represent exactly (S<<L, S=L, S>>L)?

And, if I understood correctly:

If several different forces act on the post (and not only an equally distributed load, but e.g. wind and some concentrated forces, and e.g. wind on the cameras at the top of the post, etc.) and all these forces create a moment M (marked blue in the picture below), the height h that we take in the formula will be that h (circled orange) which, when multiplied by the resultant of all the forces R (marked red) acting on the post, gives the same moment M.

While it is simpler with the fence, i.e. if it is loaded only by the distributed load from the wind w that create moment Mw, the distance of the force resultant Rw will be hw=H/2 (H=height of the fence), and also that resultant create the same moment Mw (Rw*hw = Mw).



So that in both cases the h that enters the formula

or

is the one that, when multiplied by the resultant force, gives the moment at the bottom of the post/fence, and force P in the second formula is actually resultant force that creates the same moment.

 

[FenceEng]

That is an older sketch with variable names that never got updated to match the current design guide. It's showing S as the post spacing and L as the post height and no gap at the bottom of the fencing.


For flexible fencing like chain link, if the post spacing is much smaller than the post height, the loading approaches a distributed load.

If the post spacing is equal to the height, you get concentrated loads at the top and bottom from rails or wires, and distributed triangular load from the mesh that simplifies to a point load at the mid-height.

If the post spacing is much more than the post height, the loading approaches concentrated loads, half at the top and half at the bottom. All 3 of these load cases produce a moment at the bottom of the post equivalent to a point load at the mid height. Mid rails change the distribution but the end result is equivalent.

In ASCE 7, the wind forces don't increase with height until after you pass 15' above grade, but yes, if you have forces acting at multiple heights, sum the resulting moments, divide by the sum of the forces and you'll get the IBC application height, h to use in the IBC formula in place of the (1/2 h) that I'm showing in the design guide. P would be the sum of the forces.

 

[Damned]

That is an older sketch with variable names that never got updated to match the current design guide. It's showing S as the post spacing and L as the post height and no gap at the bottom of the fencing.


For flexible fencing like chain link, if the post spacing is much smaller than the post height, the loading approaches a distributed load.

If the post spacing is equal to the height, you get concentrated loads at the top and bottom from rails or wires, and distributed triangular load from the mesh that simplifies to a point load at the mid-height.

If the post spacing is much more than the post height, the loading approaches concentrated loads, half at the top and half at the bottom. All 3 of these load cases produce a moment at the bottom of the post equivalent to a point load at the mid height. Mid rails change the distribution but the end result is equivalent.

In ASCE 7, the wind forces don't increase with height until after you pass 15' above grade, but yes, if you have forces acting at multiple heights, sum the resulting moments, divide by the sum of the forces and you'll get the IBC application height, h to use in the IBC formula in place of the (1/2 h) that I'm showing in the design guide. P would be the sum of the forces.

View attachment 4129

Thanks for all the explanations