I'm researching uncertainty calculations based on the GUM method. I have a question about estimating the standard uncertainty of an instrument based on it's calibration. In the examples I have seen, a manufacturer will quote a certain reference accuracy and state the statistical significance. Rosemount for example use 3sigma and hence it is fairly trivial to convert that to standard uncertainty given a calibration certificate.
Where I am unsure is for calibrations made on-site or in a workshop for example. Some good calibrators often display the calibration curve as well as the uncertainty associated with the calibration as in the example below for a pressure sensor.
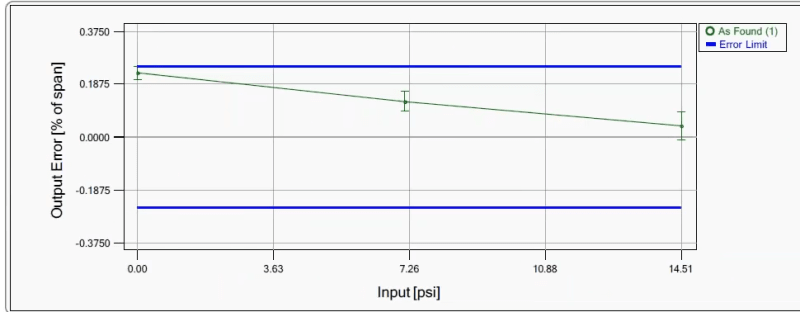
What would be an acceptable way to quote the standard uncertainty of this device's calibration in an uncertainty estimate for any measurement made by it? Is it correct to assume that since the tolerance is +/-2% of span (and is within this tolerance) that this has a rectangular probability distribution and therefore the standard uncertainty due to this calibation is derived in the usual way (2%/√3)? Is rectangular too conservative and if so, what confidence level should be applied if it were assumed to be distributed normally?
Also, does the uncertainty of the calibration process itself need to be taken into account i.e. the green error bars as shown in the figure?
Where I am unsure is for calibrations made on-site or in a workshop for example. Some good calibrators often display the calibration curve as well as the uncertainty associated with the calibration as in the example below for a pressure sensor.

What would be an acceptable way to quote the standard uncertainty of this device's calibration in an uncertainty estimate for any measurement made by it? Is it correct to assume that since the tolerance is +/-2% of span (and is within this tolerance) that this has a rectangular probability distribution and therefore the standard uncertainty due to this calibation is derived in the usual way (2%/√3)? Is rectangular too conservative and if so, what confidence level should be applied if it were assumed to be distributed normally?
Also, does the uncertainty of the calibration process itself need to be taken into account i.e. the green error bars as shown in the figure?
