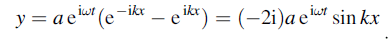Lucifer12
Mechanical
- Feb 24, 2019
- 16
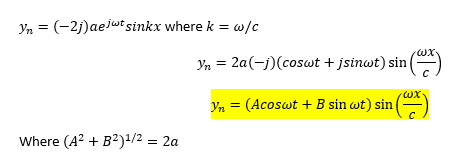
The highlighted equation. I just can, not think of a way to decompose the equation into getting A and B without getting rid of j. Any ideas?
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.