cal91
Structural
- Apr 18, 2016
- 294
I'm designing hoisting/rigging/spreader bars for picking these large modules. They give me the attachment points to the modules and where the center of gravity is. So I just need to figure out how much force is going into each pick point. Theres are large modules with 12 pick points each, and I made a spreadsheet to find the forces at each pick point. It's set up similar to a rigid diaphragm distributing shear force to vertical elements, but it's got added complexity of being two dimensional instead of 1 dimensional. Balancing the moments in the two directions interact with each other and I'm trying to figure out how to set it up correctly so that summing the moments in both directions equals zero.
I simplified the problem into this little puzzle. I'm laughing at myself because at first glance this seems so easy to solve but I'm struggling.
See if you can solve it. I know I'm having a brain fart, but I'm gonna be stubborn and not come back on until I've solved it myself.
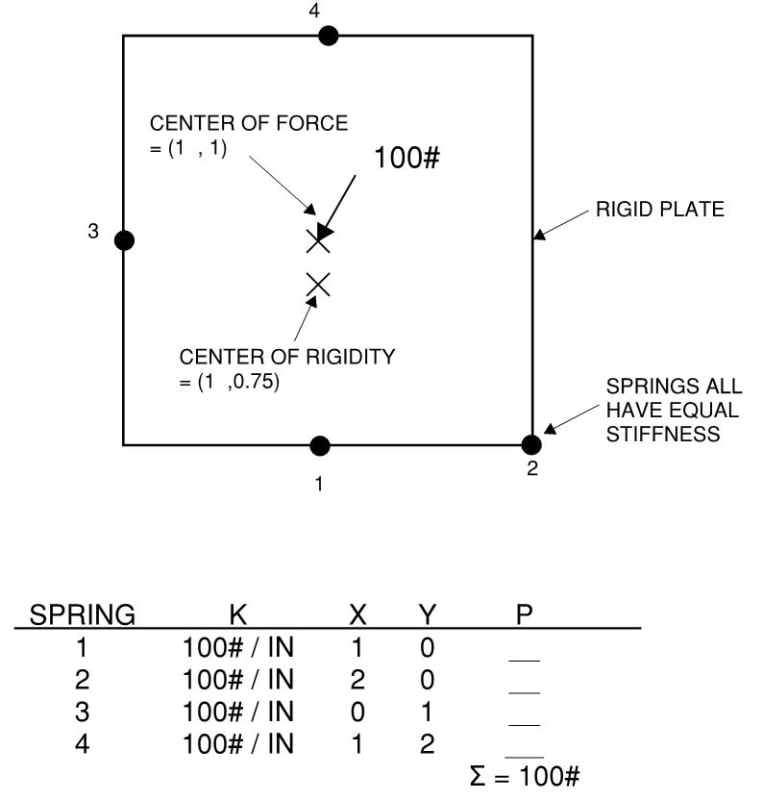
I simplified the problem into this little puzzle. I'm laughing at myself because at first glance this seems so easy to solve but I'm struggling.
See if you can solve it. I know I'm having a brain fart, but I'm gonna be stubborn and not come back on until I've solved it myself.


![[thumbsdown] [thumbsdown] [thumbsdown]](/data/assets/smilies/thumbsdown.gif)
