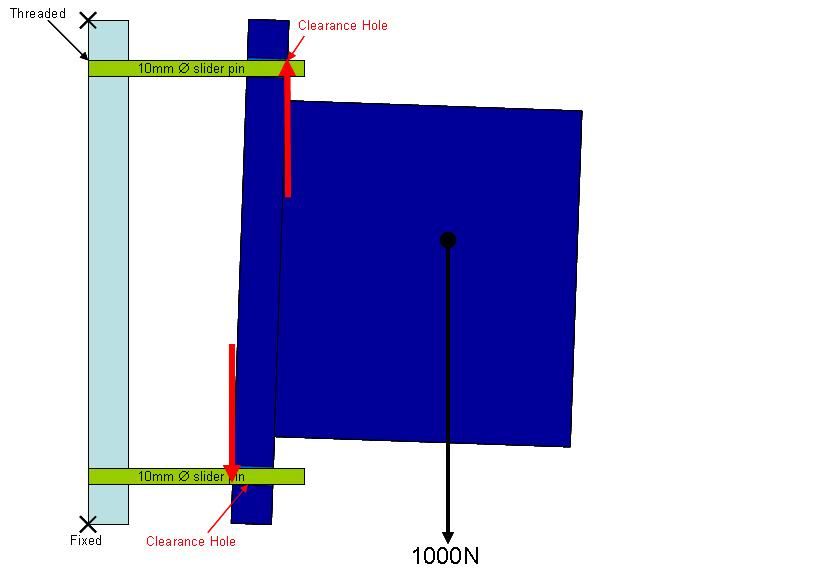
Hello,
I have a situation with a cantilevered beam with a point vertical load AND a moment load. A combination of the two following scenarios:


I did the calculations, and basically the beam will fail. So I’m wondering what will happen if I put this load on 2 beams spaced vertically apart. Will the load get split evenly between the 2 beams? Will just the vertical load get split evenly, and the moment load get greatly reduced…or disappear altogether? Will the vertical load INCREASE? Do I need FEA analysis to figure this out? Does the vertical distance between the beams make a difference?
I have posted this on another forum and have gotten confusing responses including most of the above. My instinct tells me that the vertical load will be split amongst the beams, and the moment load will be greatly diminished depending on the vertical distance between the beams. But I’m not sure. Can anyone help me understand what’s going on?
Below is a diagram I made of my situation…basically a bolted joint with all the bolts loosened and removed, except for 2. The load is free to slide back and forth on the pins.
Thank you in advance…
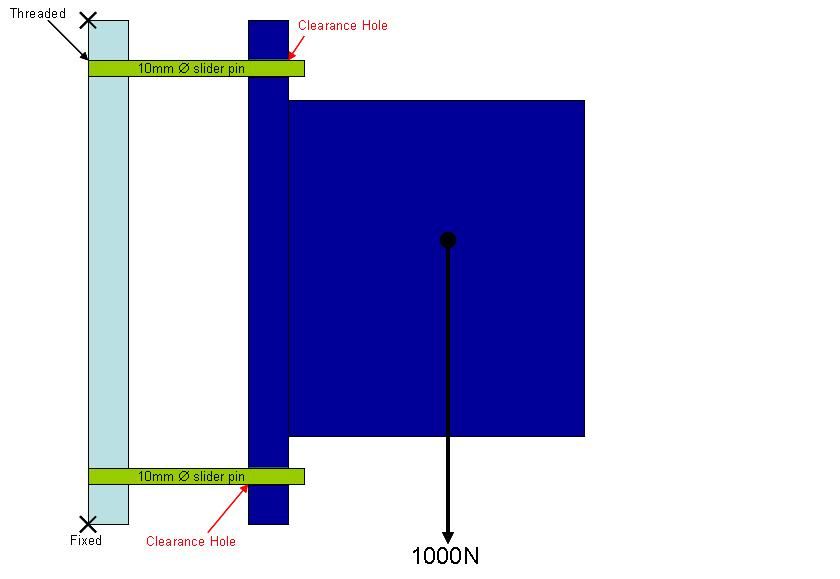
I have a situation with a cantilevered beam with a point vertical load AND a moment load. A combination of the two following scenarios:


I did the calculations, and basically the beam will fail. So I’m wondering what will happen if I put this load on 2 beams spaced vertically apart. Will the load get split evenly between the 2 beams? Will just the vertical load get split evenly, and the moment load get greatly reduced…or disappear altogether? Will the vertical load INCREASE? Do I need FEA analysis to figure this out? Does the vertical distance between the beams make a difference?
I have posted this on another forum and have gotten confusing responses including most of the above. My instinct tells me that the vertical load will be split amongst the beams, and the moment load will be greatly diminished depending on the vertical distance between the beams. But I’m not sure. Can anyone help me understand what’s going on?
Below is a diagram I made of my situation…basically a bolted joint with all the bolts loosened and removed, except for 2. The load is free to slide back and forth on the pins.
Thank you in advance…