Cantilever Beam under pure torsion - stress at fixed end?

[cohoman]

I'm looking at a cantilever beam with a pure torsion load applied at the free end. From the various references I've read, I understand that at the free end the stress is 100% torsional shear (Saint Venant's torsion). As you move towards the fixed end of the beam, the section stress is partly torsional shear stress and partly due to lateral shear as depicted in the picture below.

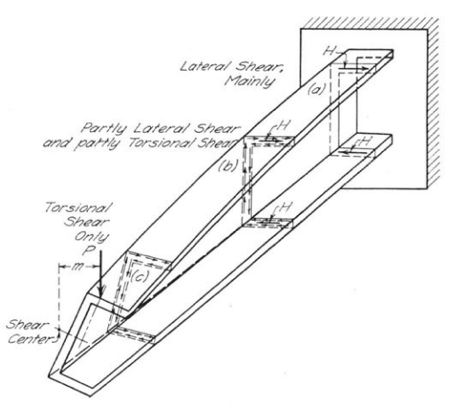
Because the flanges at the fixed end of the beam are restrained from warping the torsional stresses can't develop at that end. Instead, the applied torsional load is reacted by lateral shear forces in the flanges of a I-Beam for example, and also in-plane bending moments. I can visualize and understand this concept when looking at a I-Beam section, but what about something simpler like a slender rectangular section?

For a rectangular section of dimensions b and t, Saint Venant's shear stress due to pure torsion is calculated as 3T/(b*t^2). From my description above I understand this is the shear stress at the free end of the beam. What about the fixed end of the beam? For a rectangular section do we have the same shear stress, or is there zero shear stress? If so, how is the torsion load reacted at the fixed end?

Thanks.

 

[canwesteng]

I believe st venant torsional stresses are substantially more complicate than you make them out to be. Check out AISC design guide 9 if you need to determine torsional stresses, or build a fea model.

 

[cohoman]

My description of the section stresses in this situation comes from various reference material, so it's not my supposition. The theory makes sense to me for an I-Beam or C-channel section, but I'm not sure if this applies to a simple rectangular cross-section. I do plan to create a simple FEA model to evaluate the forces and stresses at the fixed end, but I still would like to get feedback from others who understand this situation better than I.

 

[canwesteng]

Sorry, I misread the question. For a closed section the formula for torsional stresses you have is correct. Warping stresses are negligible. An fea model is probably not required.

 

[dik]

Do a search for "sand heap analogy St. Venant torsion" to get an idea of the complexity for not circular sections.

Dik

 

[cohoman]

>> Sorry, I misread the question. For a closed section the formula for
>> torsional stresses you have is correct. Warping stresses are negligible.

So are you saying that the shear stress for a the rectangular cross-section beam under pure torsion would be 100% St Venant's shear stress (3T/(b*t^2) at the fixed end?

 

[canwesteng]

I'm going to say I'm wrong again...

 

[KootK]

So are you saying that the shear stress for a the rectangular cross-section beam under pure torsion would be 100% St Venant's shear stress (3T/(b*t^2) at the fixed end?

In practical, design office terms, yes. However, I believe that every non-circular thing warps to some degree.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

Even a circular shape will warp bit if either the load and suppprt reactions are delivered as anything other than uniform shear.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[cohoman]

Thanks for everyone's comments. If I was designing this part from scratch I probably would use the St Venant's shear stress for sizing (sssuming it would be conservative), however, in my case I'm trying to show an existing part as being good and the shear stress due to torsion is killing my margin of safety. I've read that for a beam in pure torsion the fixed end would be experiencing "differential bending" instead of shear stress, but I can't find anything to quantify that for a simple rectangular section (vrs. an I-Beam section).

I'm coming to the conclusion that I'll need to examine a detailed FEA model of a beam under torsion and try to make some correlation or judgement on the reaction loads and stresses on the fixed end.

 

[Hokie93]

The maximum torsional shear stress on a solid rectangular bar varies with the b/t ratio. For example, the "3" in 3T/bt² ranges from 4.808 for b/t = 1.0 to 3.0 for b/t = infinity. There are tabular listings of the coefficients versus b/t in many mechanics of materials textbooks and in Timoshenko's Theory of Elasticity.

 

[cohoman]

>> The maximum torsional shear stress on a solid rectangular
>> bar varies with the b/t ratio.

Yes, I understand that. I should have mentioned that the b/t ratio I'm using is >> 10, therefore the factor in that equation is 3.

 

[rb1957]

if you have b/t >>10 I won't call that a rectangle.

do you really have a long section like that ??

if you did have that section, I'd've thought that torsion (from a shear load) would be the least of your problems.

you show a pic of a beam loaded in shear (in fact shear through the shear center so no torsion) but the thread is "beam under pure torsion" ... which implies to me a beam loaded by torque ?

and, yes, I get that even a beam loaded through the shear centre can develop torsion, due to displacements, though the usual assumption is "small deflections".

another day in paradise, or is paradise one day closer ?