Kereo
Geotechnical
- Dec 10, 2018
- 8
Hey everyone:
Trivial question here, but I asked my colleague and didn't get a convincing answer
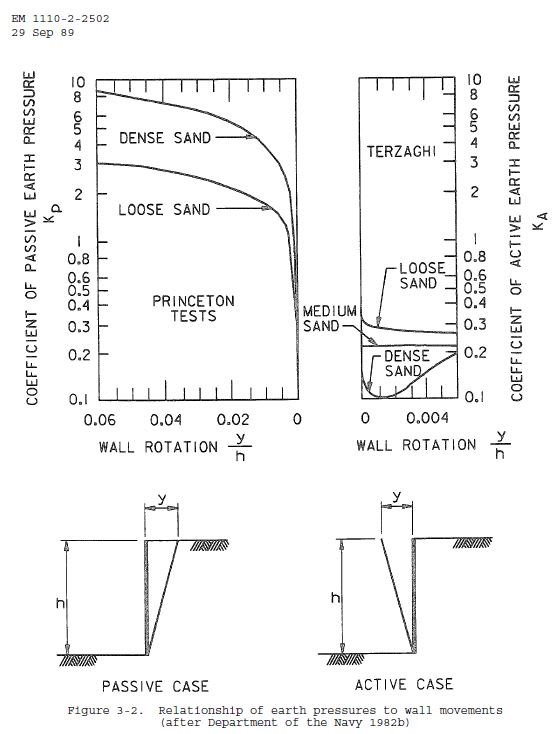
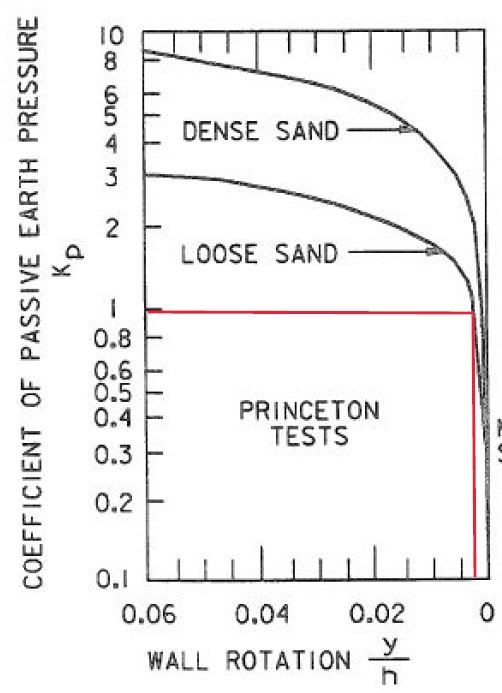
So I've recently started designing a conventional cantilever retaining wall while working through the preliminary calcs, I became aware of the K(active) and K(passive) coefficients that I'm using. I mean, I've always been taught to use these coefficients to calculate the earth pressures acting on the wall. But will the retaining wall reach these limiting states, because according to Rankine, the wall has to undergo some degree of deformation before the K(At rest) reaches one of these limiting states.
I'm not sure whether this is more conservative, because when K(At rest) approaches K(active), the active pressure gradually reduces, so wouldn't it be more conservative to design the wall at a higher "K(active)" pressure? Why do we design the wall at its failure point?
Any advice would be greatly appreciated thx
thx
Trivial question here, but I asked my colleague and didn't get a convincing answer
So I've recently started designing a conventional cantilever retaining wall while working through the preliminary calcs, I became aware of the K(active) and K(passive) coefficients that I'm using. I mean, I've always been taught to use these coefficients to calculate the earth pressures acting on the wall. But will the retaining wall reach these limiting states, because according to Rankine, the wall has to undergo some degree of deformation before the K(At rest) reaches one of these limiting states.
I'm not sure whether this is more conservative, because when K(At rest) approaches K(active), the active pressure gradually reduces, so wouldn't it be more conservative to design the wall at a higher "K(active)" pressure? Why do we design the wall at its failure point?
Any advice would be greatly appreciated