Hi all,
I am new on this forum. Im a mechanical engineering masters student.
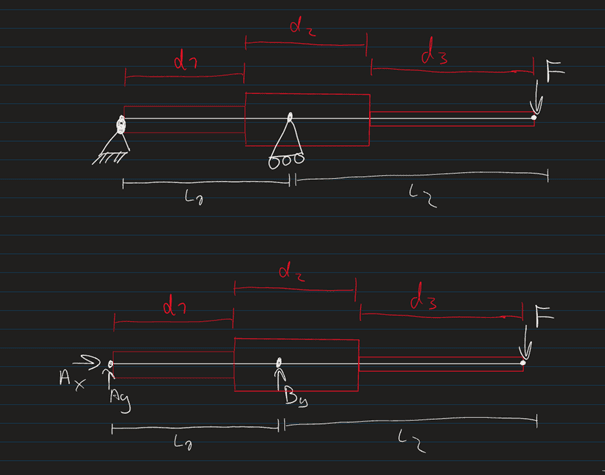
For an assignment, I am designing an overhanging beam, and optimizing it for weight.
Due to production and material choices, we went with U (channel section) beam.
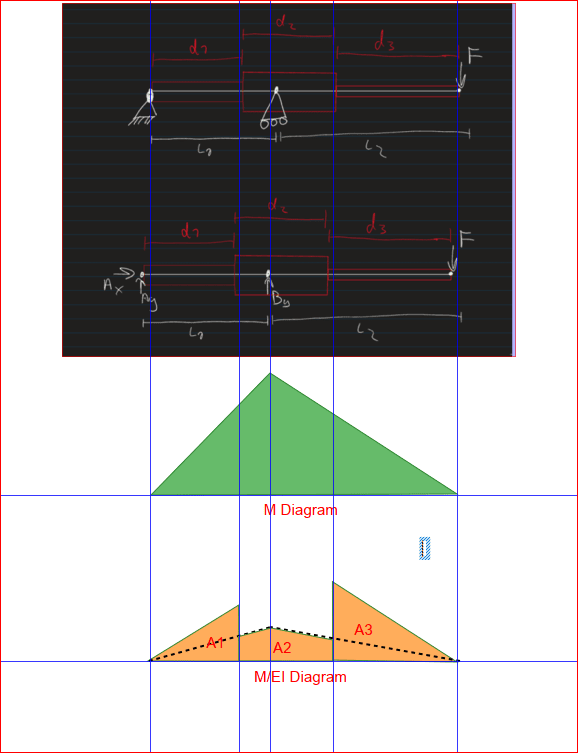
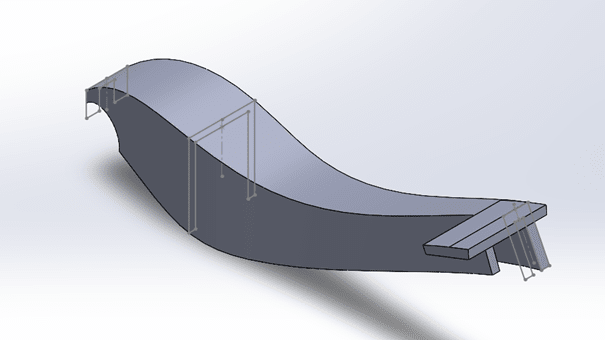
To minimize weight, I want to vary the cross section along the beam. To approximate this, I have subdivided the beam into three sections with a different cross section thus different moment of inertia, see pictures. I was getting along with the calculations, but now have 8 constants to solve for and only 6 (7 if v3=0 is counted) boundary conditions. Im also hesitant about how I set up my calculations in terms of Inertia for the second cut.
Could anyone point me in the right direction as to how to proceed?
Thanks in advance
Thanks in advance.
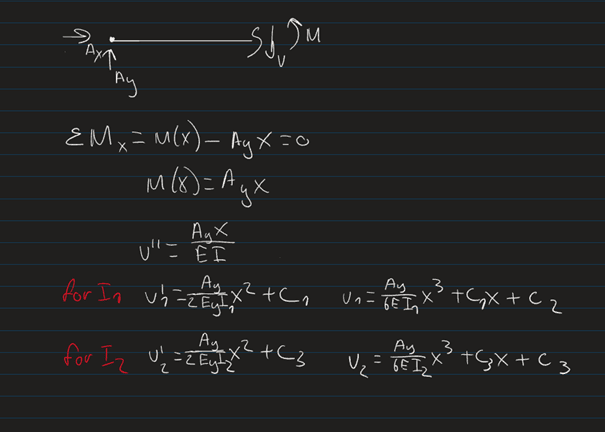
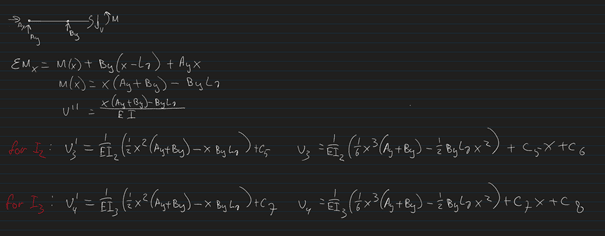
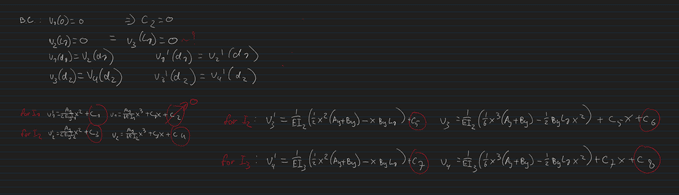
I am new on this forum. Im a mechanical engineering masters student.
For an assignment, I am designing an overhanging beam, and optimizing it for weight.
Due to production and material choices, we went with U (channel section) beam.
To minimize weight, I want to vary the cross section along the beam. To approximate this, I have subdivided the beam into three sections with a different cross section thus different moment of inertia, see pictures. I was getting along with the calculations, but now have 8 constants to solve for and only 6 (7 if v3=0 is counted) boundary conditions. Im also hesitant about how I set up my calculations in terms of Inertia for the second cut.
Could anyone point me in the right direction as to how to proceed?
Thanks in advance
Thanks in advance.

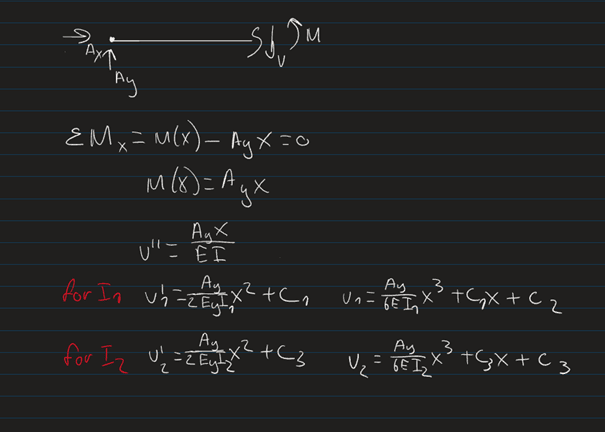
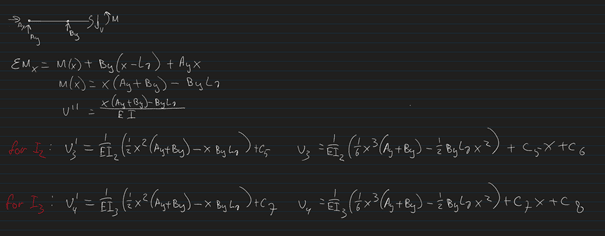
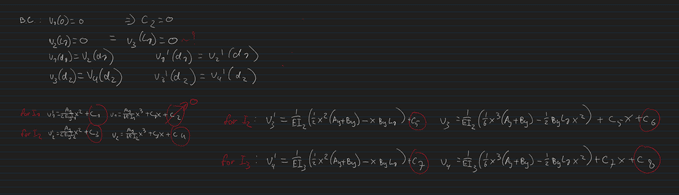

![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)