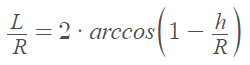Hello!
I'm having some troubles, and I really don't know if i'm over complicating. Hopefully some of you will be able to help me.
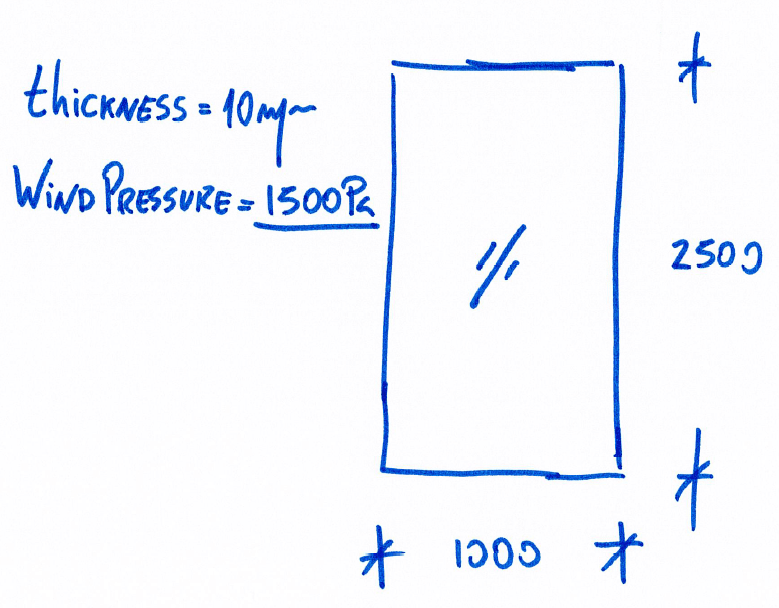
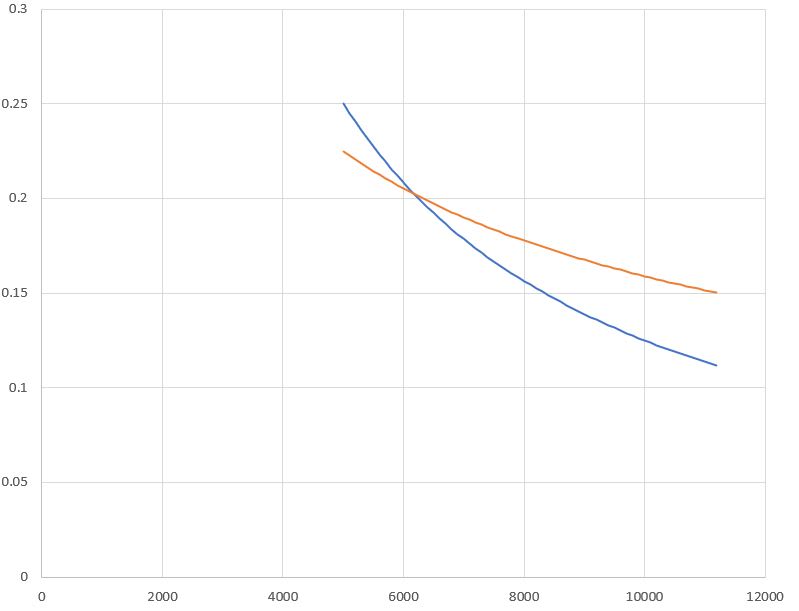
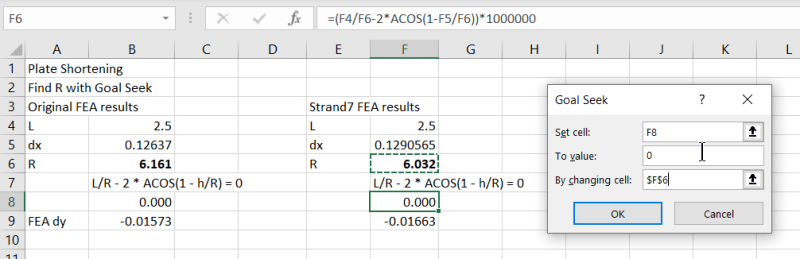
I'm currently trying to prepare some hand formulas to put on my excel sheet to evaluate the chord shortening of a glass panel when subjected to wind pressure.
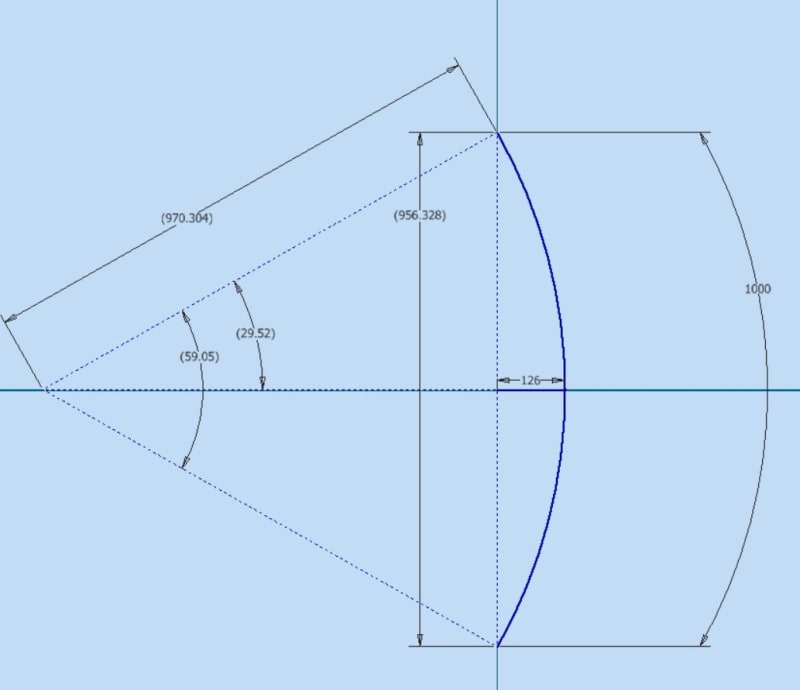
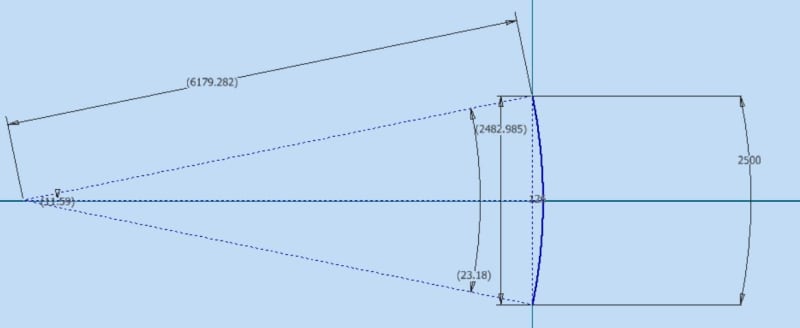
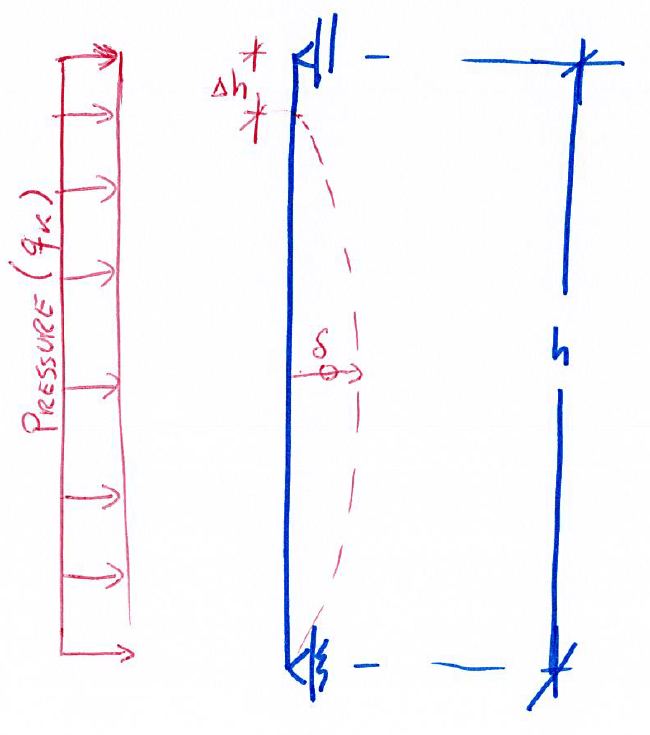
I'm able to find the deflection (δ on the scheme bellow) on the pane and I would like to backward evaluate the Δh (vertical displacement) in order to ensure the glass ply doesn't slip out of the framework.
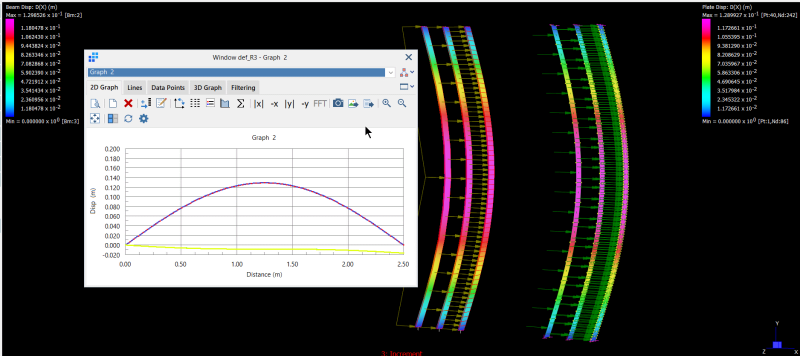
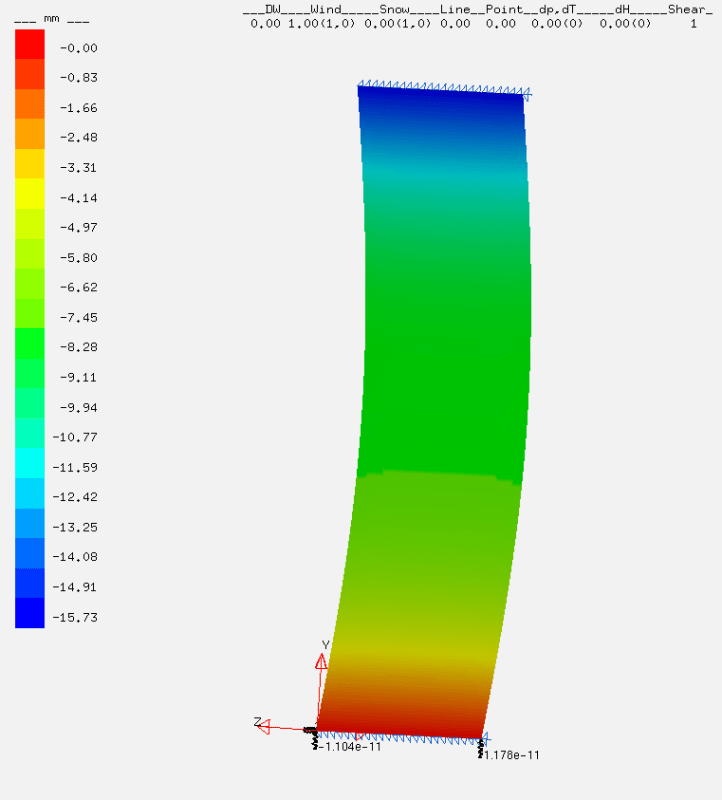
Vertical Displacement on a FEA
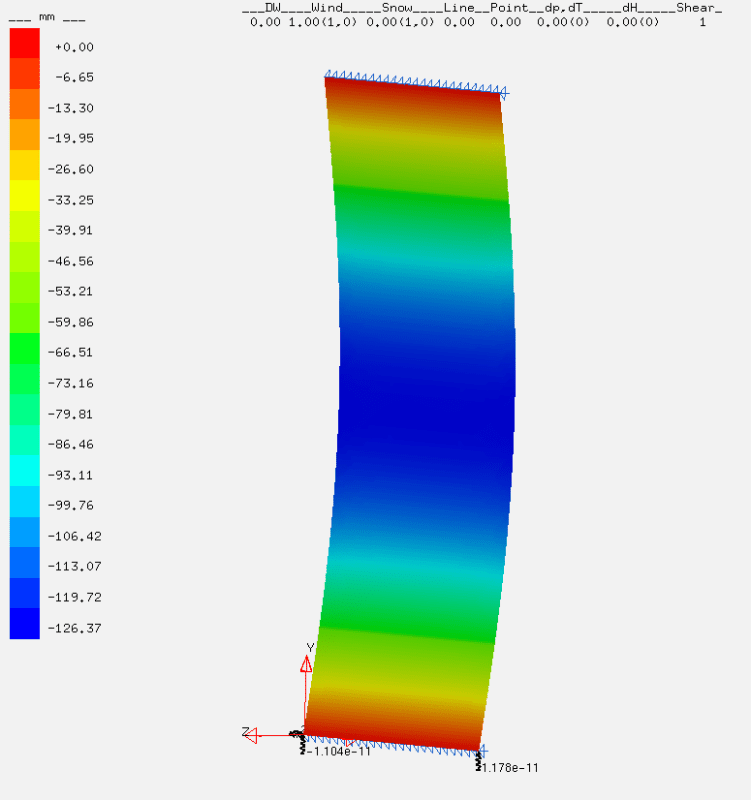
Horizontal Displacement on a FEA
I'm having some troubles, and I really don't know if i'm over complicating. Hopefully some of you will be able to help me.
I'm currently trying to prepare some hand formulas to put on my excel sheet to evaluate the chord shortening of a glass panel when subjected to wind pressure.
I'm able to find the deflection (δ on the scheme bellow) on the pane and I would like to backward evaluate the Δh (vertical displacement) in order to ensure the glass ply doesn't slip out of the framework.

Vertical Displacement on a FEA

Horizontal Displacement on a FEA