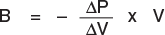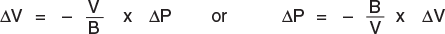gtsolid
Mechanical
- May 4, 2016
- 41
Good morning,
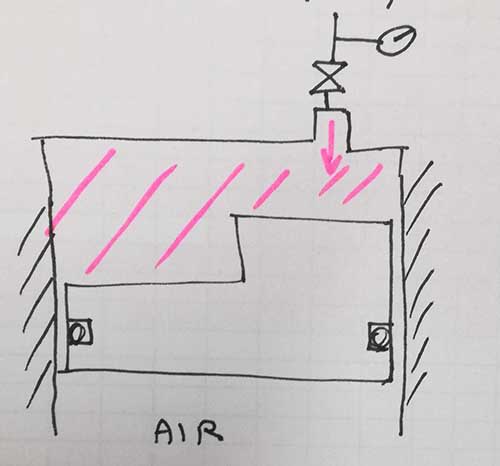
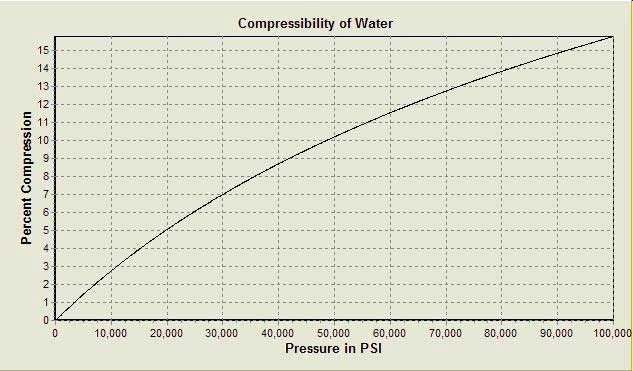
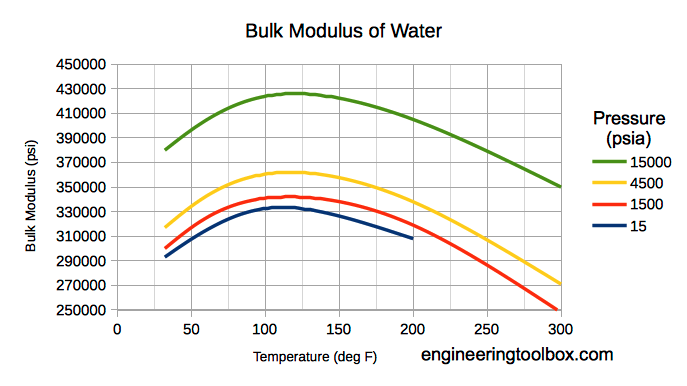
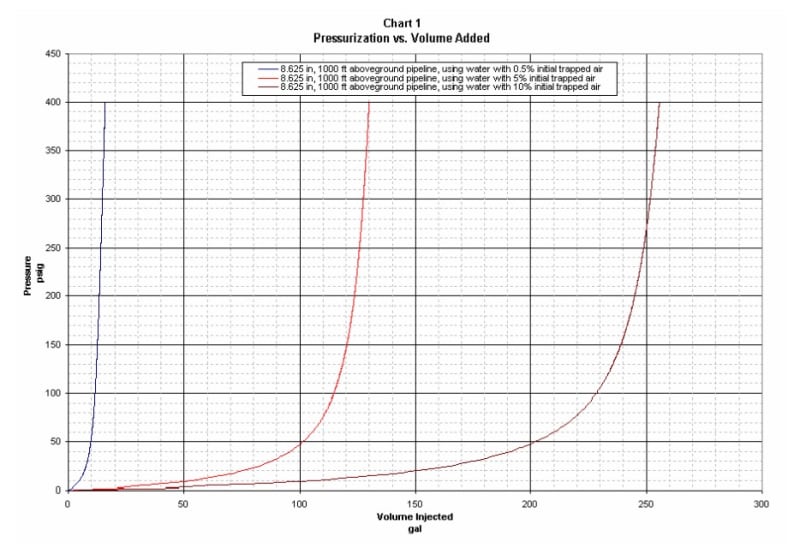
I have a fixed volume room under oil pressure. In 1 night i notice that the pressure lowers of 10%.
Can i conclude, since the oil is incompressible, that the quantity of oil remained is 10% less?
Reasoning i think it's not possible, because if i lose 0.1l of oil i think the pressure goes to 0. How can i calculate this quantity?
I have a fixed volume room under oil pressure. In 1 night i notice that the pressure lowers of 10%.
Can i conclude, since the oil is incompressible, that the quantity of oil remained is 10% less?
Reasoning i think it's not possible, because if i lose 0.1l of oil i think the pressure goes to 0. How can i calculate this quantity?