LoadSlayer
Structural
- Jan 28, 2024
- 9
Hi,
could anybody help me solve this problem? I tried to solve it and I got the answer B. But the solution key shows C.
Please see the picture below:
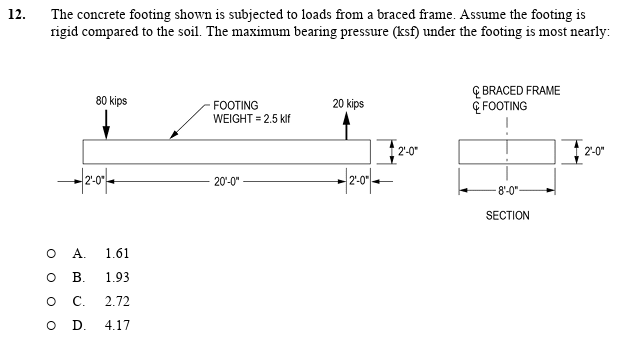
could anybody help me solve this problem? I tried to solve it and I got the answer B. But the solution key shows C.
Please see the picture below: