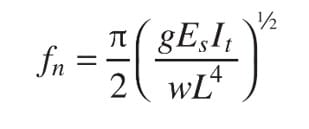composite deck slab vibrations analysis 2

[Ma.ahmed]

Good Day every one

i had to design mezzanine with big span around 30m x30m using I Built up section.
it is not allowable to use truss due to architect issues.
i had designed using Etabs and verifying by STAAD
i found that walking acceleration is safe and within limit.
but natural frequency still come = 2hz < 3hz
my question can i say that structure is safe under vibration even if natural frequency <3hz depending on walking acceleration results which is safe
thanks

 

[271828]

Can you further describe the situation? What is the occupancy? What loads were included in the natural frequency calcs? What is the slab? What are the member sizes?

 

[Ma.ahmed]

first of all thank you for you interest and responce

this is a mezzanine into exciting concrete Mall building
using deck slab com floor 120mm
for loads of SDDL 3 kn/m2 & 5 Live loads
member size main beam size is WEB 1650x20+2 flanges 400x40 with spacing 7m between concrete columns
loads considreed for natural frequancy is (Dead loads +Super dead load +0.1 live loads )
and we use UB406x140x39 as secoandry member each 1.60 m

 

[HTURKAK]

The frequency should be calculated using stiffness of gross composite section and , with loading ( G+ 0.1*Q ). The 10% LL is the imposed load portion includes ,only furnitures etc.

Pls provide some sketches etc to get better responds.
The following doc. is useful to get the concept and pls look worked examples.



Use it up, wear it out;
Make it do, or do without.

NEW ENGLAND MAXIM

 

[271828]

As HTURKAK typed, make sure you include the correct masses and use the right moment of inertia.

Include only the masses that will likely be there during the vibration event. Your live load, 0.5 kN/m2 looks about right. Maybe a little high for a mall. Your superimposed dead load (3 kN/m2 = 63 psf) is unusually high. In the US, Design Guide 11 typical recommendation for ceiling and mechanical is much lower, about 0.2 kN/m2. Use unfactored loads.

Use the fully composite transformed moment of inertia of the members, regardless of whether there are shear studs.

If your natural frequency is below 3 Hz, then the potential issue is vandal jumping. At 2.2 Hz, occupants might be able to intentionally bounce in unison with the floor motion, and really get it going. They'll think this is hilarious but your client probably won't.

Your floor is massive, so it might work even with a natural frequency below 3 Hz. In such cases, I check the floor for a small group of people trying to excite the floor. In Design Guide 11, the closest type of load is probably aerobics. In Table 5-2, the dynamic coefficient of the first harmonic is 1.5. If you consider a group of five 190 lb average adult males vandal jumping, the sinusoidal load amplitude would be (1.5)(5)(190 lb). Apply that near the middle of your floor and see what acceleration you predict. Let me know if you need help with this step.

 

[271828]

Another issue if you're using Design Guide 11 is the Chapter 4 Equation 4-1 loads are for the second through fourth harmonics; see Figure 2-4. At 2.2 Hz, the first harmonic might be able to cause resonance. Equation 2-5 is the derivation. I would replace 0.83e^(-0.35fn) with 0.4 from Table 1-1 (Willford et al. (2007) first harmonic). Use your re-derived Equation 4-1 to compute the acceleration due to a single walker on your floor.

If you're using the SCI P354, you'll need to do something similar. Equation 50 has a dynamic load factor that's appropriate for other-than first harmonic excitation.

 

[Ma.ahmed]

Thanks Mr/Ms 271828/HTURKAK
please note that the applied loads are required as per client/consultant. requiremements and as per porject specifications
as there are finished and slab covering and MEP, so these loads are required.
already i check the vibration using staad with code of AISC360-10 depending on design guide 11 for vibrations.

i found statment in DEsign giude 11 CH.4 sec4.1
"Floor systems with fundamental frequencies less
than 3 Hz should generally be avoided, because they are liable
to be subjected to "rogue jumping" (see Chapter 5)."
so i think natural frequancy must not be less than 3HZ

but if i did camber to main beam under dead loads of steel members, Can i use the resultant deflection into calculation so natural frequency EQ3.3
if Ok please provide reference

MR/MS 271828, can you please provide explanation for below part
"If you consider a group of five 190 lb average adult males vandal jumping, the sinusoidal load amplitude would be (1.5)(5)(190 lb). Apply that near the middle of your floor and see what acceleration you predict. Let me know if you need help with this step."

are you mean to add point load for (1.5)(5)(190 lb) to beam mide span and check defelction the calcutate natural frequancy. if not please provide explanation reference

thanks every on in advance

 

[271828]

please note that the applied loads are required as per client/consultant. requiremements and as per porject specifications
as there are finished and slab covering and MEP, so these loads are required.

The project specifications say you must use a superimposed dead load of 3 kN/m2 in the vibration analysis? The analysis must be run with the superimposed dead load that will probably be there during a vibration event, not one that has been set for strength/deflection design.

but if i did camber to main beam under dead loads of steel members, Can i use the resultant deflection into calculation so natural frequency EQ3.3

No, camber won't make any difference in the natural frequency. The system will vibrate about an equilibrium position that is higher than if the beam wasn't cambered. That has no effect on frequency or acceleration.

Note that the presence of Delta in the natural frequency equation is only an algebraic manipulation to make the frequency equation easier to remember. The natural frequency of a beam or girder is computed using the following equation, which is from Design Guide 11 Chapter 3. w/g is the distributed mass that would be present during vibration. The use of Delta causes never-ending confusion such as this question on camber.

[quote="If you consider a group of five 190 lb average adult males vandal jumping, the sinusoidal load amplitude would be (1.5)(5)(190 lb). Apply that near the middle of your floor and see what acceleration you predict. Let me know if you need help with this step."

are you mean to add point load for (1.5)(5)(190 lb) to beam mide span and check defelction the calcutate natural frequancy. if not please provide explanation reference][/quote]

I would predict the acceleration due to a vandal jumping group using Design Guide 11 Equation 2-1.

1. Compute the amplitude of the sinusoidal force, P = Q*alpha = (190 lb / person)(5 people)(1.5)

2. Compute the effective weight, W, using Design Guide 11 Chapter 4.

3. Compute the effective mass, M = 0.5W/g, as shown in Equation 2-5 and explained in Allen and Murray (1993), which is cited in Design Guide 11.

4. Set beta equal to whatever you are using for the walking analysis. There aren't enough people to justify the 0.06 in Design Guide 11 Chapter 5.

5. Compute the sinusoidal peak acceleration, ap = P / (2 beta M). This is nothing more than the steady-state acceleration amplitude for a viscously damped SDOF system subjected to a sinusoidal force at resonance.

6. There's no specific tolerance limit. I would start taking this case very seriously if you get over 2%g.

 

[Ma.ahmed]

Thanks, a lot for above clarifications and explanations.
really this was a valuable discussion which i got new experience in this part.
i am grateful to you

let me please come back if i faced any further problems.

thanks again

 

[271828]

You're very welcome!