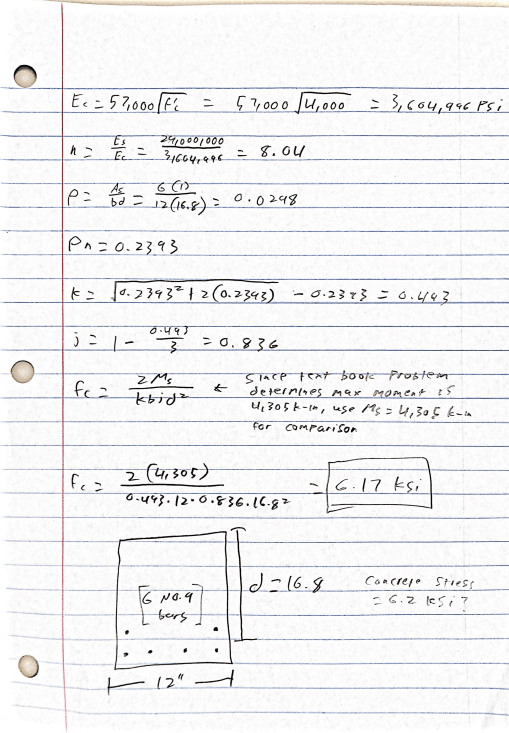I have a bit of confusion when it comes to determining the nominal moment of a simply supported reinforced beam. Personally, I have always stuck to the method of determination being shown in the book (determine the stress in the reinforcement @ concrete failure and plug it into Mn = Asfy(d-a/2)). However, I am currently studying for the PE exam and performing these calculations will be time consuming so I began looking into the PE reference manual for the "simpler method" outlined as shown in the screenshot. You'll note that if you use these methods, you'll get vastly different Mn determinations.
As a check to see if these moments line up, I plugged in the correct Mn shown in the book into and I am getting a concrete stress of 6.17 ksi (when f'c = 4 ksi). So my question is this: why do I get such different values with each method? Should I set the maximum concrete force in the second method to 4 ksi? If this is done, it will result in Mn showing a value of only 2791 k-ft (65% of the value determined in the first method). Thanks for any insights you may be able to provide.
Textbook solution (determination of stress in reinf)
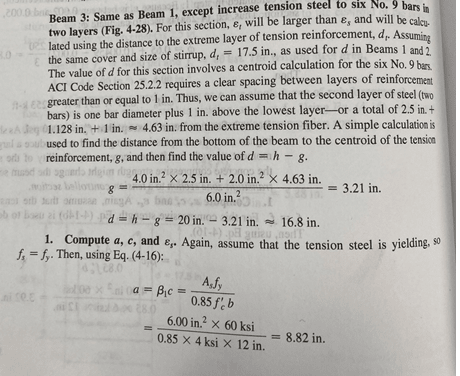

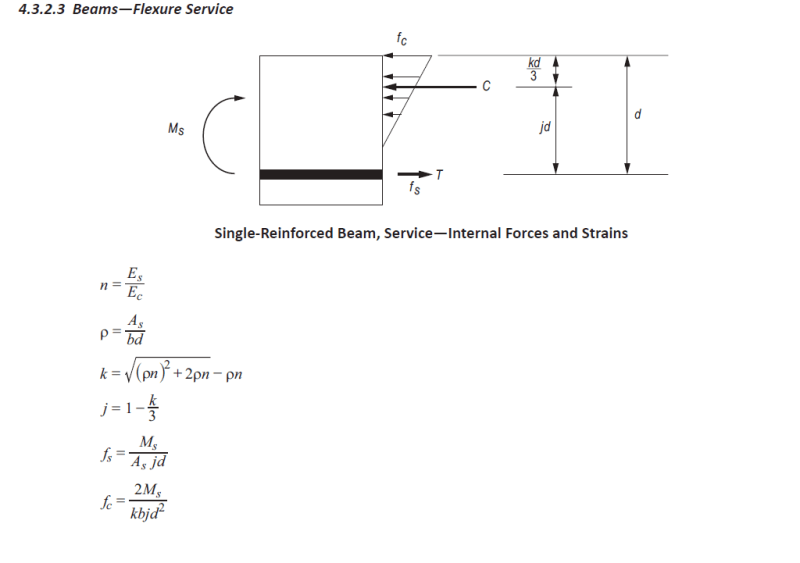
PE Handbook solution
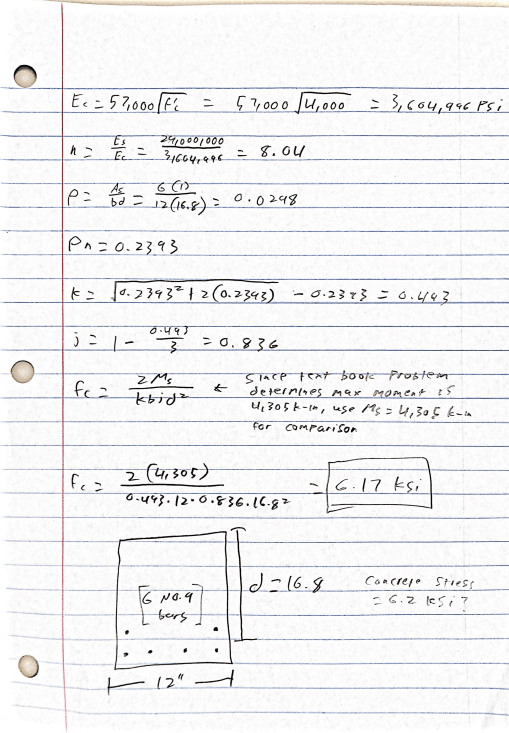
As a check to see if these moments line up, I plugged in the correct Mn shown in the book into and I am getting a concrete stress of 6.17 ksi (when f'c = 4 ksi). So my question is this: why do I get such different values with each method? Should I set the maximum concrete force in the second method to 4 ksi? If this is done, it will result in Mn showing a value of only 2791 k-ft (65% of the value determined in the first method). Thanks for any insights you may be able to provide.
Textbook solution (determination of stress in reinf)
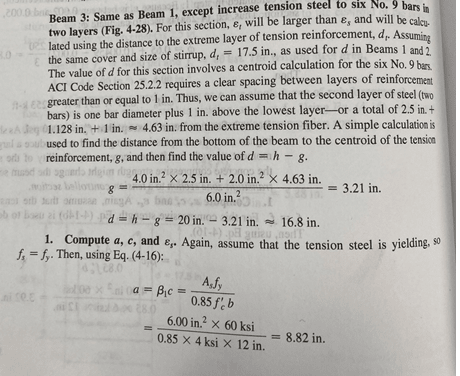

PE Handbook solution