Concentrated Load on CMU Wall

[Nulukkizdin]

Just wanting to confirm my interpretation of the code for a masonry question I have. For reference, I'm currently looking at the 2008 masonry design code, so I know the verbiage will be slightly different between years.

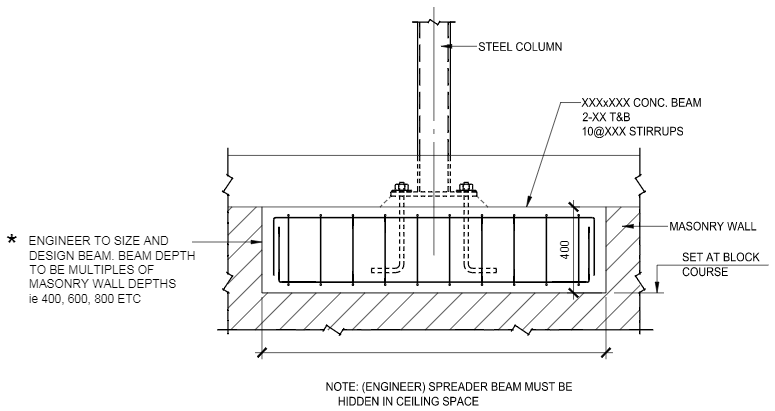
My condition involves a steel beam bearing on a plate which sits atop a CMU wall with a running bond. In checking the capacity of this bearing condition, my design will include 1) the bearing check of the concentrated load on the CMU and 2) the effective wall panel itself resisting the compression load.

For part 1, section 1.9.5 (2008 version) notes that the bearing area is a function of the loaded area and any distribution for a concentric load. For simplicity, if my bearing plate is the full width of the wall, I would think that taking the concentrated load divided by the baseplate area would be the value to compare against 0.25*f'm.

For part 2, section 1.9.7 (2008 version) describes a distribution of a 2:1 slope to half height of the wall. Again for example a 10' high wall with a 12" wide baseplate would give an effective length of 12" + 2*(60/2) = 72". With this in mind I could take my concentrated load and check a 72" wide wall panel to resist it. This would obviously change if the 2:1 distribution is truncated by a wall end or adjacent load.

Anyone want to chime in on this? My main concern here is resisting the bearing load of a large concentrated force. Seems like the only solution for a really big load would be increasing the baseplate size significantly or bumping up my f'm?

Thanks!

 

[jike]

Don't forget that you will need to require the cores to be grouted solid below the beam bearing. The depth and width of the grout can be varied depending on how heavy the load is.

 

[jike]

If the load gets too heavy, you always have the option of putting a column in the wall. I have also seen some engineers put a short distribution beam under the main beam to distribute the load to the wall over a longer length.

 

[KootK]

Here are a couple of details for the distribution beam concept.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

I should also add that, for commonly proportioned distribution beams, I've always been skeptical about just how much distribution occurs. Think beam on very stiff elastic springs.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[EngineeringEric]

I do not think you want to bump up f'm. I would suggest the larger plate, or a spreader beam.

I agree with your reading of the code sections FYI.

 

[Nulukkizdin]

Thanks for the responses. As noted I am planning on grouting the cores per the typical beam and am providing columns in many of the locations of higher load. Any thoughts on the code interpretation or if I'm missing something (besides Eric - thanks for confirming)?

 

[JLNJ]

I'm with KootK in that I doubt that there is much spreading going on here other than a 45 degree distribution. More likely is that the local stresses in the masonry are way higher than the .25F'm you are hoping for. Whether this would cause a local failure, I don't know.

I had a similar discussion with a young engineer who was finding that the longer she made the bearing plate under a beam (parallel to the wall) the thicker the plate needed to be. I tried to convince her that no matter HOW long she made the plate, most of the forces will be concentrated right under the load and most the plate wouldn't "activate". The same for me is true with column base plates.

 

[KootK]

The same for me is true with column base plates.

I did an FEM investigation of this way back and came to the same conclusion. Base plate thickness need to be ridiculous in order to generate anything resembling a uniform bearing pressure. I've come to accept that some degree of material crushing below the base plate hot spots is required to allow these things to function successfully.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.