Concrete column design: Equation 4

[Pretty Girl]

The following equation to get the moment of the compression force (Mc) is mentioned in the "Reinforced Concrete Design to Eurocodes" by prab bhatt on page 353.

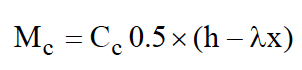
My question is:
Is the "0.5" number mentioned in that is the neutral axis? can we use 0.7 instead of 0.5? I noticed if we use higher number for that, we can reach higher moment resistances.
But I'm not sure if the "0.5" is for the neutral axis or not.

 

[IDS]

Why would you use 0.7?

For a column (or any section with combined bending and axial force) you take moments about the centre of the section, for all the forces, not the Neutral Axis.

The "centre" is taken as the centroid of the uncracked concrete section (ignoring the effect of the steel), because that is where the member is assumed to be located in a structural analysis.

For a rectangular section with a rectangular stress block the lever arm from compression centroid to section centre = h/2 - lambda.x/2.

If you are using a parabolic-linear stress block, or any other non-linear shape, you should calculate the position of the stress block centroid.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Pretty Girl]

For a rectangular section with a rectangular stress block the lever arm from compression centroid to section centre = h/2 - lambda.x/2.

Thank you for the reply.

So, it should be safe to only change the neutral axis to be 0.7 or whatever we want it to be, and keeping the 0.5 lambda.x as it is?
I mean, is it possible to use 0.7 for only the "h/2" part? it should still be safe isn't it?

So, lever arm = (0.7 x h - 0.5 x lambda.x ) --> this is also a safe design isn't it?

Examples:

= (0.7 x h - 0.5 x lambda.x )
= (1 x h - 0.5 x lambda.x )
= (1.25 x h - 0.5 x lambda.x )

all of the above should be safe as we're only changing the neutral axis isn't it?

and why should we take moments from the centre of the column? why not from the just the edge of the column? or exceed the column? I feel like the column can even be designed to have a neutral axis outside the column like 1.25h than 0.5h. When lambda.x reaches height of the column the neutral axis is outside the column. Am I wrong?
Please let me know why is it unsafe to design a column which is having a neutral axis lies outside the column height (eg: 1.25h)?

 

[NedGan76]

You cannot just decide by yourself where the centroid of a section is. It is determined by the laws of physics (mechanics). For a rectangular section it is at z = h/2. That's it. The question about if anything else is "safe" or not is irrelevant, because it is simply wrong.

However, when checking the bending capacity (MEd < MRd) you can choose a different point. But you must also re-calculate your design loads as well. If you choose your point at the edge of the column, then you have to increase the design bending moment: MEd,edge = MEd + NEd*h/2. But it will not make any difference. If MEd > MRd, you will also get MEd,edge > MRd,edge.

 

[dik]

I've attached a publication I used to do my conc col spreadsheet (actually used for spreadbored with a moment applied). The same approach can be used for a rectangular column.

[URL unfurl="true"]https://res.cloudinary.com/engineering-com/image/upload/v1690826941/tips/Circular-Reinforced-Concrete-Column-Interaction-Diagram-ACI318-14_oimwxl.pdf[/url]

-----*****-----
So strange to see the singularity approaching while the entire planet is rapidly turning into a hellscape. -John Coates

-Dik

 

[IDS]

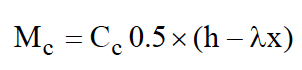
My question is:
Is the "0.5" number mentioned in that is the neutral axis?

I should have answered the question.

The answer is no, the 0.5 is not the factor for the depth of the neutral axis, it is the factor for the depth of the uncracked concrete centroid.

The depth of the neutral axis = x, so the depth of the centroid of the concrete stress block = lambda.x/2 (for a rectangular stress block).

The depth of the uncracked concrete centroid for a rectangular section = h/2.

So the equation is taking moments about the uncracked concrete centroid, which is the standard procedure.

As NedGan76 said, you can take moments about wherever you want, but if you choose to use something other than the concrete centroid you have to adjust the applied moment to be taken about the same point, so why would you do that?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[BridgeNerdGuy]

I just want to second the resource dik shared. I used an earlier version of that same file to set up my circular reinforced concrete column excel sheet that generates the interaction diagrams. I've had great success comparing my excel diagrams/capacities/results to software output for bridge piers and drilled shafts over the years.

 

[Pretty Girl]

You cannot just decide by yourself where the centroid of a section is.
But you must also re-calculate your design loads as well. If you choose your point at the edge of the column, then you have to increase the design bending moment: MEd,edge

But isn't it possible to adjust the dimensions so the neutral axis lies at an exact distance for a given design moment (Med)? when you keep reducing the column height (h) it increases the distance to neutral axis and column becoming from partially compressed to fully compressed. When lambdaX becomes 1 and neutral axis becomes 1.25, provided lambda is 0.8 and lambdaX is 0.4. So in that case, we have effectively set the neutral axis to wherever we want it to be. Isn't it correct? (Provided the concrete area already sufficient to resist axial load)

 

[Pretty Girl]

@dik
Thank you so much, I will read through the paper.

 

[Pretty Girl]

but if you choose to use something other than the concrete centroid you have to adjust the applied moment to be taken about the same point, so why would you do that?

If you can set the neutral axis to where you want, you can save on concrete as I see. You can reduce the column section height (h). if you set the neutral axis to 1.25 that means lambdaX becomes 1, and 1 means we're fully utilising the 100% of column are as compressive element than 40% of column area when the neutral axis was 0.5. Reducing dimensions may increase the savings(provided the reduced size sufficient to resist axial load).
Isn't that correct?

 

[Pretty Girl]

@BridgeNerdGuy
Thank you for your reply

 

[IDS]

If you can set the neutral axis to where you want,

But you can't. The position of the NA is governed by the applied loads and the cross section dimensions and reinforcement. You don't have any say in where the NA will be for any given cross section and applied loads.

You can choose where you take moments about, but you have to use the same point for the applied bending moment and the section capacity. That's why it makes sense to take moments about the axis used for calculating the applied moments, which is normally the centre of the section, which will usually not be the neutral axis.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/