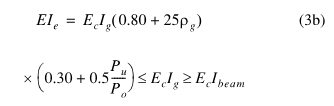Concrete Frame Second-Order Analysis (Not the Moment Magnification Method) 4

[StrEng007]

My question involves the analysis and design of concrete moment frames used to support both gravity and lateral wind loads. Although there are many posts about utilizing the moment magnifier procedure, I can't find as many resources on the approach for second-order analysis utilizing computer methods.

Excuse the long message... Hopefully I can incite some feedback from KootK, JAE, phamENG (or any other opinion, you're all valued here!).

To get us started, I'd like to briefly outline (3) procedures for how ACI 318-11 treats slenderness effects:
(Taken from Design of Reinforced Concrete, 9th Edition, McCormac/Brown)

1. Nonlinear second-order analysis (ACI 10.10.3).

Although ACI provides a nice statement about this procedure, I don't fully grasp what it means. I feel as though the statement in 10.10.3 is not very clear or beneficial for the person who actually practices. I understand this to be a computer model that captures 2nd order effects and must "predict ultimate loads within 15 percent of those reported in tests of indeterminate reinforced structures." I don't find this very helpful (I could start an entire blog about our material Codes and the need to simplify them for the practicing engineer).

How many of you are utilizing this approach?

2. Elastic second-order analysis (ACI 10.10.4).

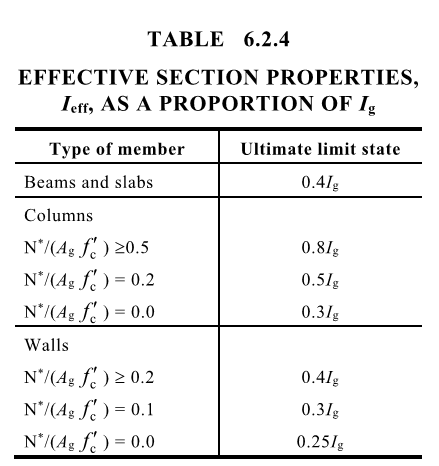
I understand this to be an approach that utilizes reduced section properties to capture the load distribution and second-order effects of members prior to failure. Since concrete is assumed to crack, we must take into account the reduction in the inertias of our members. This is the procedure I'd like to discuss in further detail.

Is it safe to assume that the majority of us are taking this approach? With tighter schedules, increasing demand on the structural engineer, and a relative compensation that hasn't shifted much from the 1980's, I find this approach to the be quickest non-academic exercise. Thoughts?

3. Moment magnification procedure (ACI 10.10.5).

This method is no stranger to this blog. It has been discussed many times from various points of view.



Now that we've covered the (3) methods, let's further discuss method #2.

For my case, I have a concrete moment frame that is supporting both gravity loads (D, Lr, L) and lateral wind loads (W). In my computer model (IES Visual Analysis), I've set the program to perform a P-Delta analysis of the frame, and modified the stiffness of columns to utilize 70% of the strong and weak moments of inertia, Iz and Iy, respectively. Additionally, the beams in the frame utilize 35% of the strong moment of inertia, Iz. These factors are applied through Section 10.10.4.1. My understanding of how this model should be run for Strength Design:

1. Create model with columns, beams, boundary conditions, associated reinforcing, applied loads, and applicable load combinations.
2. Limit the beam and column moment of inertia per Section 10.10.4.1. Again, my option for doing this is to apply reductions via a "Stiffness Factor"
Applied to Columns

Applied to Beams

3. Run the analysis, which includes P-Delta effects. This in combination of the fact that section reductions were applied, should satisfy the Elastic second order effects required per ACI. Correct?

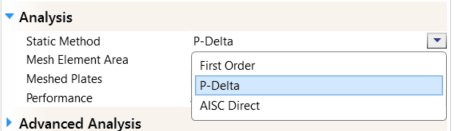
4. Verify that members have adequate strength (unity check) per the f'c and reinforcing provided within each member.

So far so good. Did I miss anything?

Now for my serviceability and deflection checks:
After achieving a successful strength design model of my frame, I create a separate copy so I can run my deflection checks.
1. Apply service load combinations (ie, ASD load combinations).
2. Per Section R10.10.4.1, in order to check service load deflections with unfactored loads, it is permissible to modify the "reduced" section properties that were applied in the strength design model. I would apply the following logic:

Columns were reduced to 0.70 Iz and 0.70 Iy
Multiplying these by 1.43, (1.43)(0.70Iz) = 1.0Iz (and the same for 1.0 Iy)

Beams were reduced to 0.35 Iz
Multiplying by 1.43, (1.43)(0.35Iz) = 0.50Iz
3. Next I re-run the analysis with the redefined section properties and investigate my deflections.

After going through ACI multiple times to review this topic, the steps above seem pretty straight forward. I would appreciate any feedback if there are some glaring mistakes in the approach I'm taking.

 

[EZBuilding]

I have never seen a practicing engineer utilize a nonlinear second-order analysis for the design of a building. Would love to be shown some examples otherwise.

Did I miss anything?

P-Delta is broken up into both Big P-Delta and Little P-Delta. Your analysis software is likely addressing big p-delta, however it may not be capturing the little p-delta effects. It is common for the little p-delta procedures of moment magnification to be performed within the elastic second order analysis. There is some literature online about "breaking up" your frame elements to allow the computer program to capture the little p-delta within the analysis. The moment magnification approach is often more punishing and I lean towards using it.

I have not designed a reinforced concrete moment frame building in practice. Nonetheless, I do question the use of a 0.7 crack factor for your columns. I expect the stresses in your columns to be higher than the modulus of rupture and also expect that the column will be more "cracked" than a "cracked shear wall" per ACI crack factors. I believe you should run some sensitivity studies to determine the impacts that a lower stiffness of your columns has on your building. Running through the values for your columns based on Table 6.6.3.1.1 should give you a good gut check.

I just tried to find it in ACI318-14 but could not, however I believe there is a limit to the maximum amount of P-Delta moment allowed. I believe this check should be perform for both little and big P-delta. In the past I've seen 1.4 be the limit for P-Delta moments. (ACI 318-11 has this limit in 10.10.2.1)

 

[centondollar]

So far so good. Did I miss anything?

I second what EZBuilding wrote about the second moments of area. The code may recommend 0.7*I_gross, but it doesn't make it realistic. To estimate it more correctly, you could run a moment-curvature calculation (available in some softwares in their concrete design module, or easily programmed for a rectangular member) to find a cracking moment and secant flexural stiffness, and then find I_cr by dividing EI_secant_cr with E.

Furthermore, if you do not have earthquakes (deflections increase forces significantly) or large deflections, the strength check should be doable without modifying section properties. This is a result of the lower bound theorem of plasticity: if you calculate internal forces with an elastic solution and reinforce the sections with plastic theory, the resistance is always adequate. The reasoning in a nutshell: maximum load that the member can attain is always bounded from above, because when most members have cracked, there is no more load redistribution (stiffness difference driven by cracking), and the internal forces will be the same as for an uncracked frame analysis. Only the deflections and natural frequencies will change.

Now for my serviceability and deflection checks:
After achieving a successful strength design model of my frame, I create a separate copy so I can run my deflection checks.
1. Apply service load combinations (ie, ASD load combinations).
2. Per Section R10.10.4.1, in order to check service load deflections with unfactored loads, it is permissible to modify the "reduced" section properties that were applied in the strength design model. I would apply the following logic:

Columns were reduced to 0.70 Iz and 0.70 Iy
Multiplying these by 1.43, (1.43)(0.70Iz) = 1.0Iz (and the same for 1.0 Iy)

Beams were reduced to 0.35 Iz
Multiplying by 1.43, (1.43)(0.35Iz) = 0.50Iz
3. Next I re-run the analysis with the redefined section properties and investigate my deflections.

Why do you increase the section stiffness for serviceability analysis? If anything, you should use reduced stiffness (leading to larger deflections) for the serviceability checks. Increasing second moments of area for serviceability is certainly un-conservative.

Do also remember that creep reduces the elastic modulus (by over 50% in some cases), which will further reduce all member flexural stiffnesses: EI_cracked = E_creep*I_cracked = 0.5*E*0.7*I , for example.

If you model plates, their stiffness can be modified by modifying the elastic modulus, and the appropriate multiplier (or even an appropriate methodology to determine it) is still a subject of research as far as I know.

 

[Celt83]

For Elastic Second Order you'll need to subdivide the members to capture along the length effects, most software packages will allow this with RAM Structural System being one of the bigger players where it is not possible. ACI does allow you to capture this effect using the non-sway magnification procedure however there is conflicting information about whether or not to use K,sway in this procedure for frames the ACI MNL-17 example manual uses K,sway but every example from the software suppliers uses K,non-sway.

As EZBuilding mentioned there is still the verification that the second order moments be less than 1.4 times the elastic moments so you'll need to run the model at least twice for strength design to confirm, this can get tricky for columns that had near 0 moments under the first order analysis and ACI doesn't provide any real guidance on this.

 

[RobertHale]

Your approach to analysis is sound. As everyone else has pointed out, make sure you are including the "along member" p-delta effects with either segmentation or application of the Non-sway B1 factors. As for deflection, my firm tries to short-change the "parallel model" approach as much as possible. We create specific load cases for wind serviceability checks, we use a 10-year MRI wind with a H/400 limit. Every once in a while we bump the MRI up higher, but the default is to keep with the 10-year wind. We will check the drift of the cracked frames with P-delta against this limit. If it works with this condition, then we just move on. Otherwise, we start by turning off the second-order effects, then using an unmodified stiffness, a few times (on existing buildings) we have gone through the laborious process of looking at stresses and doing a manual iterative analysis. As O read the code, these methods only really apply to wind loads. The drift limitations for seismic have to be done under the Design seismic load with the cracked member properties.

I have done a limited number of analyses using non-linear hinges. Others can correct me if I am wrong, but I think this classifies as Method 1. I think I have actually "double-dipped" by applying the hinges and reducing the stiffness of the columns and beams. I applied this method for progressive collapse, but I think the seismic PBD using the same ASCE 41 hinges would also classify as Method 1. I think there are plenty of engineers working with both static and dynamic non-linear analyses, especially as you move west of the Rockies.

 

[StrEng007]

Hmm.... I seem to be more confused now then when I submitted my post.

I found a similar thread where the points I discussed align with each other.

The role of Cracked Stiffness in Analysis and Design
thread507-427904

I think you can do what you (and 10.10) suggest:
1. Set up a model and adjust the moments of inertia down per 10.10.4.1 (ACI 318-11) and analyze using factored load combinations. Design for strength.
2. Take your same model, but then adjust your moments of inertia back up by 1.43. Then use unfactored combinations to check for serviceability criteria.
3. So in essence you do have two different models - one with reduced stiffnesses for strength design and one with less reduced or non-reduced stiffnesses for serviceability design.

The code may recommend 0.7*I_gross, but it doesn't make it realistic

Why does ACI permit the use of these values in 10.10.4.1 if they aren't realistic?

To estimate it more correctly, you could run a moment-curvature calculation (available in some softwares in their concrete design module, or easily programmed for a rectangular member) to find a cracking moment and secant flexural stiffness, and then find I_cr by dividing EI_secant_cr with E

This sounds time consuming and I'm not sure where I would begin. Are there worked examples that walk us through these steps? Again, I'm relying on ACI and the fact they explicitly permit the use of the values through 10.10.4.1

Why do you increase the section stiffness for serviceability analysis? If anything, you should use reduced stiffness (leading to larger deflections) for the serviceability checks. Increasing second moments of area for serviceability is certainly un-conservative.

I'm following ACI R10.10.4.1. My understanding is that using the 0.70 and 0.35 is fine for the analysis at the factored level. However, in reality for service level deflections, it's over conservative to use the 0.70/0.35 and we're allowed to increase them.

I don't deal with reinforced concrete moment frames that much, so a lot of the comments here are heavily theoretical. I'm trying to find the most direct approach to completing this analysis.

 

[EZBuilding]

Why does ACI permit the use of these values in 10.10.4.1 if they aren't realistic?

Good question - but it might be that those values were recommended with the idea that these column members would not be the primary lateral framing system in a building.

I'm following ACI R10.10.4.1. My understanding is that using the 0.70 and 0.35 is fine for the analysis at the factored level. However, in reality for service level deflections, it's over conservative to use the 0.70/0.35 and we're allowed to increase them.

I don't deal with reinforced concrete moment frames that much, so a lot of the comments here are heavily theoretical. I'm trying to find the most direct approach to completing this analysis.

I agree with you here and disagree with centondollar. It is appropriate to increase the anticipated moment of inertia for service level checks as the anticipate cracking will be lower due to the lower anticipated loading.

 

[Settingsun]

1. Nonlinear second-order analysis (ACI 10.10.3).

Although ACI provides a nice statement about this procedure, I don't fully grasp what it means. I feel as though the statement in 10.10.3 is not very clear or beneficial for the person who actually practices. I understand this to be a computer model that captures 2nd order effects and must "predict ultimate loads within 15 percent of those reported in tests of indeterminate reinforced structures." I don't find this very helpful (I could start an entire blog about our material Codes and the need to simplify them for the practicing engineer)

This is a framework that's provided so the code doesn't disallow the use of advanced methods of analysis if someone wants to use them. There are many ways to skin this cat so they can't all be spelled out in the code. Some textbooks touch on it if the author has a particular interest in the subject, otherwise you go to specialised publications from industry bodies or academic literature.

The other methods of analysis are the code simplifications for the typical practising engineer/project.

2. Elastic second-order analysis (ACI 10.10.4).

I haven't had to use ACI for some time, but bookmarked the link below in case it's specified for an international project. Might be useful as background reading.

https://www.eng-tips.com/viewthread.cfm?qid=457880

The code may recommend 0.7*I_gross, but it doesn't make it realistic

Why does ACI permit the use of these values in 10.10.4.1 if they aren't realistic?

Here are the Australian stiffness modifiers for cracked sections, for comparison. When columns don't have heavy compression, the stiffness becomes similar to a beam because the column is functionally similar to a beam in that case.

ACI 318-19 also provides alternative - image below. Not sure how the Table 6.6.3.1.1(b) equation plays out in practice. The axial force increases I_eff in one term but reduces it in another.

There's also a comment that walls should initially be analysed as 0.7*I_gross, then re-run with 0.35*I_gross if they crack. Not sure why the same doesn't apply to columns. Perhaps an unwritten assumption that the columns are braced?

It is appropriate to increase the anticipated moment of inertia for service level checks as the anticipate cracking will be lower due to the lower anticipated loading.

I do the same because it's generally accepted, but it involves an assumption that loading above nominal service loading hasn't occurred in the past. Once the concrete is cracked, the tension stiffening is lost.

 

[Settingsun]

Turns out the source articles for that ACI equation are available online:
Theory -

https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/19126

Experiments -

https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/51685169

Note that there's an error in Equation 6 of the theory paper. It's supposed to be "...+0.5*Pu/Po" (instead of subtraction). It's correct in the experimental article, where it's called equation 3b (image below). Looks like the Australian code is similar to this simplification, which is only accurate at the ultimate limit state, ie when you're sitting on the interaction curve, not inside the curve.

The theory paper has tables that show how the equations vary with the inputs over fairly typical ranges, but the maximum eccentricity considered is 0.8*section depth. Sway frames may go outside that.

 

[Lomarandil]

I designed a number of buildings similar to this over the last several years (concrete moment frames for gravity and wind load, no real seismic).

Yes, the general approach you're describing is appropriate according to the code. I also agree that including some intermediate nodes (quarter points usually works well) will capture P-d moment effects.

As for column stiffness -- yes 70% is allowable per ACI, but I agree that this isn't realistic for moment frames except in the lower stories of a building. I often perform a first analysis run, then adjust the stiffness of columns downward according to the compressive stresses (either through the more detailed ACI method, or applying the Australian provisions for simplicity).

My approach for serviceability matches Robert's.

 

[centondollar]

I agree with you here and disagree with centondollar. It is appropriate to increase the anticipated moment of inertia for service level checks as the anticipate cracking will be lower due to the lower anticipated loading.

The cracking moment for typical reinforced concrete beams, columns and slabs is negligible. Typically, cracks occur at beam mid-spans, at supports (with continuous members) and in columns (moment joints) at service loads and even at loads below them. Once the cracks occur in normal reinforced concrete, they don't close, and the inertia is permanently reduced. With these details in mind, I do not quite understand your line of reasoning.

 

[Settingsun]

More cracks at ultimate reduces the tension stiffening compared with service load.

 

[JoshPlumSE]

I thought I'd throw my $0.02 in here on some of the OP's questions as well as some responses:

Is it safe to assume that the majority of us are taking this (Elastic 2nd order analysis) approach?

Yes, I think that's probably a safe assumption.

As a review of StrEng007's procedure:

Your procedure for doing the 2nd order analysis is pretty much what I would do. However, I have to re-iterate EZBuilding's comments about the difference between P-Big Delta and P-little delta. And, how you MIGHT need to subdivide your columns between floors in order to fully account for p-little delta.

 

[centondollar]

Your procedure for doing the 2nd order analysis is pretty much what I would do. However, I have to re-iterate EZBuilding's comments about the difference between P-Big Delta and P-little delta. And, how you MIGHT need to subdivide your columns between floors in order to fully account for p-little delta.

If the software uses the geometric stiffness method, there is no separate "P-Big Delta" and "P-little delta"; the full p-delta is captured automatically along a member, with greater accuracy as element length is reduced. On the other hand, some software use equivalent nodal shear, and in that case, "subdivision" of some kind might be needed.

 

[JoshPlumSE]

centondollar -

There are multiple ways to incorporate P-Delta.
1) Using secondary shears: This only applies at joint locations. I know that RISA-3D used to work this way. I'm not sure of any other programs that do that.
2) Geometric stiffness adjustment: This method does NOT guarantee that this will account for both types of P-Delta.
a) This can be done to only account for joint translation in which case, it is (like method 1) only accounting for P-Big Delta, and would still require sub-division.
b) If the geometric stiffness adjustment accounts for BOTH nodal translation and nodal rotation, then yes it will account for both Big Delta and little delta effects. However, I would suggest that even if the software claims to do this, that you would be wise to test it out first. Specifically comparing it to the "benchmark" examples in the AISC commentary.

 

[EZBuilding]

The cracking moment for typical reinforced concrete beams, columns and slabs is negligible. Typically, cracks occur at beam mid-spans, at supports (with continuous members) and in columns (moment joints) at service loads and even at loads below them. Once the cracks occur in normal reinforced concrete, they don't close, and the inertia is permanently reduced. With these details in mind, I do not quite understand your line of reasoning.

This comes straight from ACI. Reference ACI 318-14 6.6.3.2.2 and it's commentary.

I believe this comes from an understanding that the building code requires strength levels of performance during a strength design wind event - not serviceability performance.

 

[slickdeals]

Here is a process that I have for slender columns in ETABS.

Run a linear static second order analysis with column Ig set to 0.7 to capture effect of cracking (ACI 6.7.1.1 recommends 0.875).

Divide member along height to capture local effects (ACI 6.7.1.2). This is done by selecting the frames in the tall floor -> Assign -> Frame -> Frame AutoMesh and then selecting it to divide into a number of segments. Usually I go with 4.
Section properties in member definitions should be accordance with ACI 6.6.3.1. (typically we set it to 0.7 for Ig)

1. Run Iterative P-Delta analysis. (global stability). Use load combination 1.2D + 0.5 L.
2. Divide tall floor column into multiple segments to capture P-little delta (ACI 6.7.1.2). I have verified that ETABS captures P-little delta effects from member deformations when a P-Delta analysis is run in the program.
3. Run the analysis and compare the values from second order analysis (P-delta on) versus first-order analysis (P-delta off) and confirm that ratio of second order to first order moment is less than 1.4 (ACI 6.2.5.3)
4. Assign columns as non-sway (shear wall building) and then manually override delta_ns factor to 1.01 or 0.99 to bypass OS#20 warning.
5. Accidental eccentricities effects are accounted in the ACI strength equations. See commentary R22.4.2.1.
6. Turn on "consider minimum eccentricity" to add some additional factor of safety on top of the program calculated moments. (This is not required when following ACI 6.7)

As an additional check, calculate critical buckling load (P c) using a reduced EI_eff computed using (0.4*Ec*Ig)/(1+Beta_dns). Check to see if you have at least FoS of 2 (arbitrary at this point).