Similar to the subject here thread507-463800, I have been concerned in the past about the shear capacity being compromised due to a lack of flexural reinforcing and excessive cracking. I don't see anything in ACI that addresses it. So, for example if there is no top slab reinforcing in the thread above, would that affect the shear capacity of the slab assuming a crack propagates a distance away from the support?
Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Concrete shear capacity-no flexural reinforcing 1
- Thread starter haynewp
- Start date
rowingengineer
Structural
Most codes have allowances for minimum shrinkage and temperature reinforcing to ensure the concrete behaves as expected such that the rules in the code can be applied.
"Programming today is a race between software engineers striving to build bigger and better idiot-proof programs, and the Universe trying to produce bigger and better idiots. So far, the Universe is winning."
"Programming today is a race between software engineers striving to build bigger and better idiot-proof programs, and the Universe trying to produce bigger and better idiots. So far, the Universe is winning."
rowingengineer
Structural
I should have included crack control as well
"Programming today is a race between software engineers striving to build bigger and better idiot-proof programs, and the Universe trying to produce bigger and better idiots. So far, the Universe is winning."
"Programming today is a race between software engineers striving to build bigger and better idiot-proof programs, and the Universe trying to produce bigger and better idiots. So far, the Universe is winning."
haynewp - I guess I've always thought that if there was adequate flexural reinforcement on the bottom, extending into the support as required by ACI, then the shear of the section based on ΦVc would be determined and compared with Vu a distance "d" from the support....for slabs.
For beams it would be ΦVc/2 and for joists it would be ΦVc/2 x 1.1.
If Vu was over ΦVc/2 for beams, I'd have to put in minimum stirrups of course.
For the slab condition you referenced, if the slab cracked over the support then assuming proper bottom slab reinforcement I'd be OK with the slab shear capacity assuming a nice straight saw cut over the beam to ensure the cracking didn't wander out past the edge of the support. If it did, then that section where the cracking got out past the support would indeed give me worry.
For beams it would be ΦVc/2 and for joists it would be ΦVc/2 x 1.1.
If Vu was over ΦVc/2 for beams, I'd have to put in minimum stirrups of course.
For the slab condition you referenced, if the slab cracked over the support then assuming proper bottom slab reinforcement I'd be OK with the slab shear capacity assuming a nice straight saw cut over the beam to ensure the cracking didn't wander out past the edge of the support. If it did, then that section where the cracking got out past the support would indeed give me worry.
-
1
- #7
haynewp said:
1) I've shared a similar concern for a long, long time. And you and I aren't the only ones as, I assure, I did not CAD up the sketch below for your benefit.
2) A subtly different but related issue - for me at least - is that our codes often separate the design of shear from the design of moment for functional reasons and, in doing so, make it easy for designers to forget that shear and moment resistance must be supplied in a mutually compatible fashion so as to tell a cohesive story of load carrying capacity.
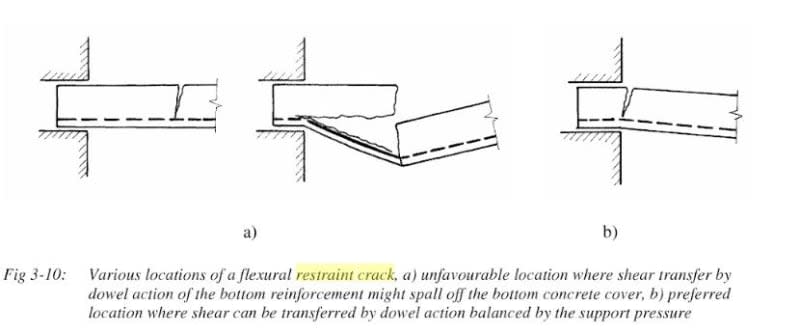
Considering pure theory, I agree with KootK. You do need to look at both shear and flexural together and how they are related.
From a practical side, really, how often do one-way slabs fail in shear? There is so much redundancy in a one-way slab and we neglect things such as the slabs torsional rigidity.
A continuous beam without top reinforcing and relying only on Phi*Vc is a different story.
From a practical side, really, how often do one-way slabs fail in shear? There is so much redundancy in a one-way slab and we neglect things such as the slabs torsional rigidity.
A continuous beam without top reinforcing and relying only on Phi*Vc is a different story.
So all of KootK's images show my reference to a "wandering" crack extending out beyond the edge of the support.
That all makes perfect sense and I'd be very concerned about a slab with a crack at, or just outside the support edge.
What the OP was asking in the post that haynewp referenced was about a slab cracking and should, or rather could, they saw cut over the support such that there was still bearing on the support and no cracking outside that bearing. I'd feel a lot better about that.
That all makes perfect sense and I'd be very concerned about a slab with a crack at, or just outside the support edge.
What the OP was asking in the post that haynewp referenced was about a slab cracking and should, or rather could, they saw cut over the support such that there was still bearing on the support and no cracking outside that bearing. I'd feel a lot better about that.
- Thread starter
- #10
The saw cutting certainly helps but, even with that, I'd not consider this issue sufficiently resolved. I'd not want people's safety resting on whether or not a crack formed where I asked it to even if I did provide some positive encouragement. We attempt this on a regular basis with slabs on grade and look how reliable that is.
I'm also not willing to put much stock in the absence of one-way slab shear failure out in the wild. In 99% of those cases, in continuous concrete structures, we do put top steel in to reflect where we expect negative moments to materialize near supports. If you look at any of the great, old school concrete design aids, they almost always specify top steel as a minimum ratio of bottom steel even if you're pretending the supports are pinned.
I have an uncommon amount of experience with this situation:
1) Where I live, there was a period in time where a consultant was designing one way roof slabs on bearing walls and intentionally omitting the top steel because a) it saves material and b) who cares if the top of a roof slab cracks? I've looked at a couple of these buildings. They'll have flexural cracks near, but not always right over, the walls. No shear problems.
2) I did a forensic thing for a two-way slab building on the west coast where top mats were specified at the columns but, somehow, they didn't get installed in about half of the locations where they were specified. Lots of cracking and... wait for it... no two way shear failures.
I have another, related concern with respect to all forms of strut and tie design. This will sound ridiculous but bear with me. Suppose I design my ties to suit a particular strut angle but then the concrete decides that it would like to form cracks, and therefore struts, at a different angle. Concrete, like me, is notorious for being a bad listener. This would result in the strut missing my tied node altogether. Thanks to the capricious nature of my strut, everybody dies right? Obviously not. But why not? And, whatever the answer is, how can I trust it?
My current theory is that this is rectified by considering how internal stresses will develop from the point of zero stress to ULS. Hopefully, the strut will form at an angle connecting my tied nodes because the tied nodes represent points of increased internal stiffness even before cracks form. The the struts would stay there post cracking. One might postulate that a similar mechanism would encourage your critical shear resisting struts to form cracks over bearing points rather than beside bearing points.
I know, as I write this stuff I also wonder if I should be allowed to design things given the depth of my ignorance.
I'm also not willing to put much stock in the absence of one-way slab shear failure out in the wild. In 99% of those cases, in continuous concrete structures, we do put top steel in to reflect where we expect negative moments to materialize near supports. If you look at any of the great, old school concrete design aids, they almost always specify top steel as a minimum ratio of bottom steel even if you're pretending the supports are pinned.
I have an uncommon amount of experience with this situation:
1) Where I live, there was a period in time where a consultant was designing one way roof slabs on bearing walls and intentionally omitting the top steel because a) it saves material and b) who cares if the top of a roof slab cracks? I've looked at a couple of these buildings. They'll have flexural cracks near, but not always right over, the walls. No shear problems.
2) I did a forensic thing for a two-way slab building on the west coast where top mats were specified at the columns but, somehow, they didn't get installed in about half of the locations where they were specified. Lots of cracking and... wait for it... no two way shear failures.
I have another, related concern with respect to all forms of strut and tie design. This will sound ridiculous but bear with me. Suppose I design my ties to suit a particular strut angle but then the concrete decides that it would like to form cracks, and therefore struts, at a different angle. Concrete, like me, is notorious for being a bad listener. This would result in the strut missing my tied node altogether. Thanks to the capricious nature of my strut, everybody dies right? Obviously not. But why not? And, whatever the answer is, how can I trust it?
My current theory is that this is rectified by considering how internal stresses will develop from the point of zero stress to ULS. Hopefully, the strut will form at an angle connecting my tied nodes because the tied nodes represent points of increased internal stiffness even before cracks form. The the struts would stay there post cracking. One might postulate that a similar mechanism would encourage your critical shear resisting struts to form cracks over bearing points rather than beside bearing points.
I know, as I write this stuff I also wonder if I should be allowed to design things given the depth of my ignorance.
KootK:
Fixed it for you
1) Where I live, there was a period in time where a consultant was designing one way roof slabs on bearing walls and intentionally omitting the top steel because a) it saves material and b) who cares if the top of a roof slab cracks? I've looked at a couple of these buildings. They'll have flexural cracks near, but not always right over, the walls. No shear problems [red]yet[/red].
2) I did a forensic thing for a two-way slab building on the west coast where top mats were specified at the columns but, somehow, they didn't get installed in about half of the locations where they were specified. Lots of cracking and... wait for it... no two way shear failures [red]yet[/red].
Fixed it for you
1) Where I live, there was a period in time where a consultant was designing one way roof slabs on bearing walls and intentionally omitting the top steel because a) it saves material and b) who cares if the top of a roof slab cracks? I've looked at a couple of these buildings. They'll have flexural cracks near, but not always right over, the walls. No shear problems [red]yet[/red].
2) I did a forensic thing for a two-way slab building on the west coast where top mats were specified at the columns but, somehow, they didn't get installed in about half of the locations where they were specified. Lots of cracking and... wait for it... no two way shear failures [red]yet[/red].
- Status
Similar threads
- Locked
- Question
- Locked
- Question
- Locked
- Question
