azureblue83
Structural
- Jan 26, 2015
- 17
Load Combination 5 and 7:
1.2D+1.0E+L+0.2S
0.9D+1.0E
where D is defined as simply "dead load" and E = earthquake load, calculated as following:
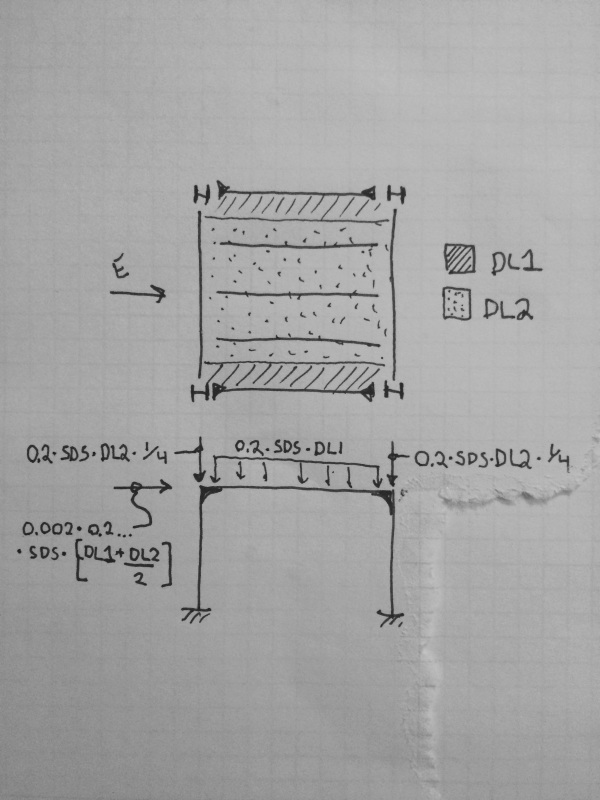
E = Eh +- Ev = pQE +- 0.2SDSD
where QE is the effect of horizontal seismic effect, and 0.2SDSD is the vertical seismic effect.
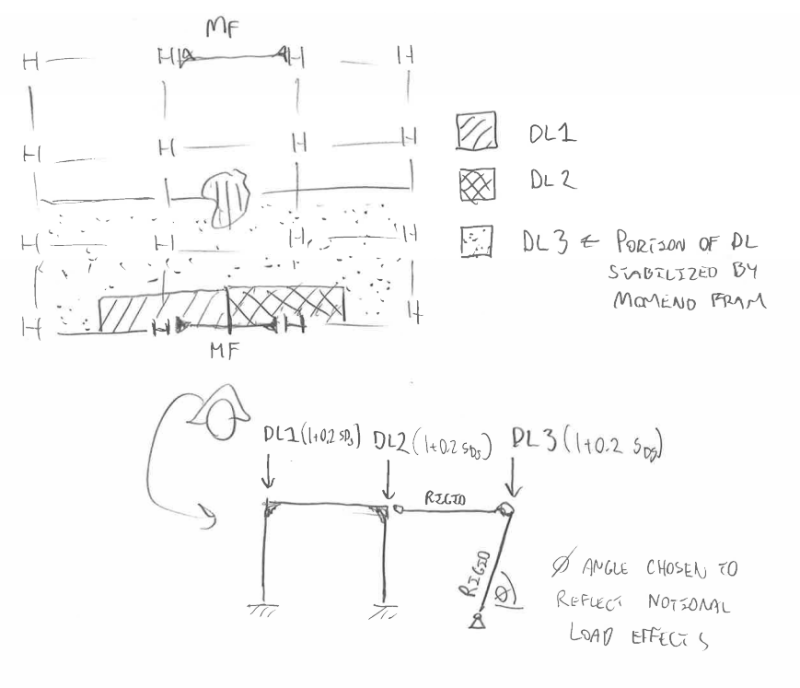
Now, suppose designing a moment frame that is for lateral load only, i.e. it is not taking any dead/live load except its self weight, but it is taking seismic lateral load due to building's dead load. What "D" should be used for the 0.2SDSD? Do we use the building's D? Or, just the moment frame's self weight D?
1.2D+1.0E+L+0.2S
0.9D+1.0E
where D is defined as simply "dead load" and E = earthquake load, calculated as following:
E = Eh +- Ev = pQE +- 0.2SDSD
where QE is the effect of horizontal seismic effect, and 0.2SDSD is the vertical seismic effect.
Now, suppose designing a moment frame that is for lateral load only, i.e. it is not taking any dead/live load except its self weight, but it is taking seismic lateral load due to building's dead load. What "D" should be used for the 0.2SDSD? Do we use the building's D? Or, just the moment frame's self weight D?