Structural noob
Structural
Hey all,
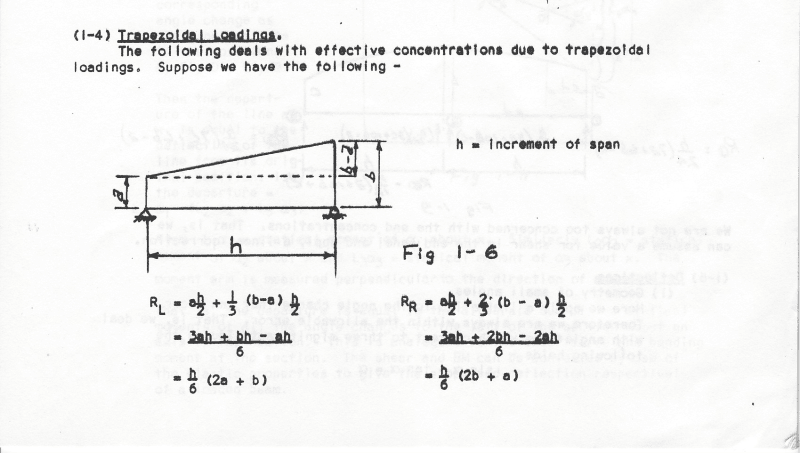
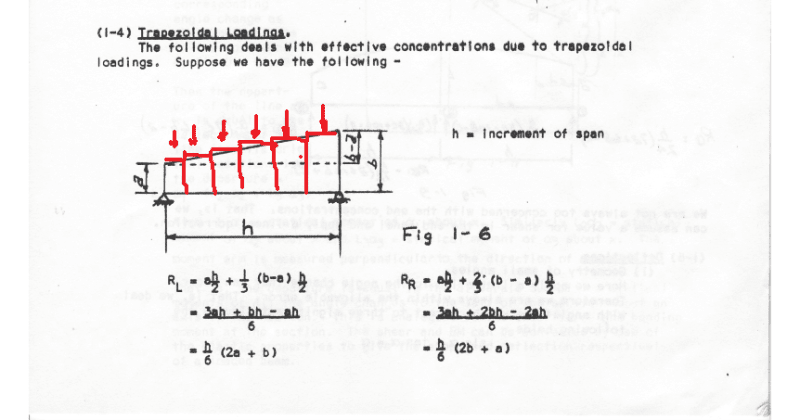
I wanted to know if there is any way I can convert a trapezoidal load to point loads at regular intervals so that I can demonstrate that as a moving load?
Thank you
I wanted to know if there is any way I can convert a trapezoidal load to point loads at regular intervals so that I can demonstrate that as a moving load?
Thank you