271828
Structural
- Mar 7, 2007
- 2,283
Greetings all! I have what is probably a silly question, but I'm having a hard time figuring it out, so here goes.
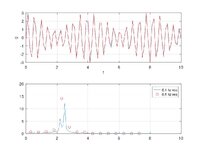
I have an acceleration magnitude spectrum with a constant resolution of 0.125 Hz (call this Spectrum #1). These are steady-state vibrations in a building, mostly from mechanical units, so there are a few fairly isolated peaks. I need to convert Spectrum #1 to an equivalent spectrum (Spectrum #2) with a 0.5 Hz resolution.
Would it be reasonable to do this based on energy, as described below?
For example, consider the 5 Hz center frequency.
271828
I have an acceleration magnitude spectrum with a constant resolution of 0.125 Hz (call this Spectrum #1). These are steady-state vibrations in a building, mostly from mechanical units, so there are a few fairly isolated peaks. I need to convert Spectrum #1 to an equivalent spectrum (Spectrum #2) with a 0.5 Hz resolution.
Would it be reasonable to do this based on energy, as described below?
For example, consider the 5 Hz center frequency.
- In Spectrum #2, this bin goes from 4.75 Hz to 5.25 Hz.
- In this same range of frequencies, Spectrum #1 has points at 4.75 Hz, 4.875 Hz, 5 Hz, 5.125 Hz, and 5.25 Hz.
- The energy of each Spectrum #1 point would be the acceleration magnitude squared times 0.125 Hz. (Half that at 4.75 Hz and 5.25 Hz because the other half goes into the adjacent 4.5 Hz and 5.5 Hz bins, respectively.)
- Sum the energy for the five points to get E at 5 Hz.
- The Spectrum #2 magnitude at 5 Hz would be sqrt(E / 0.5 Hz).
271828
Last edited: