I am working on a large industrial machine on frictional skid rails (i.e., 1 dimension of movement is possible on the rails). As its motor starts up, it begins to vibrate the machine around 20Hz; i.e., movement occurs on the frictional rails. The phenomenon is similar to what is shown in the YouTube video HERE. This is quite similar to Coulomb's damping scenario (images below).
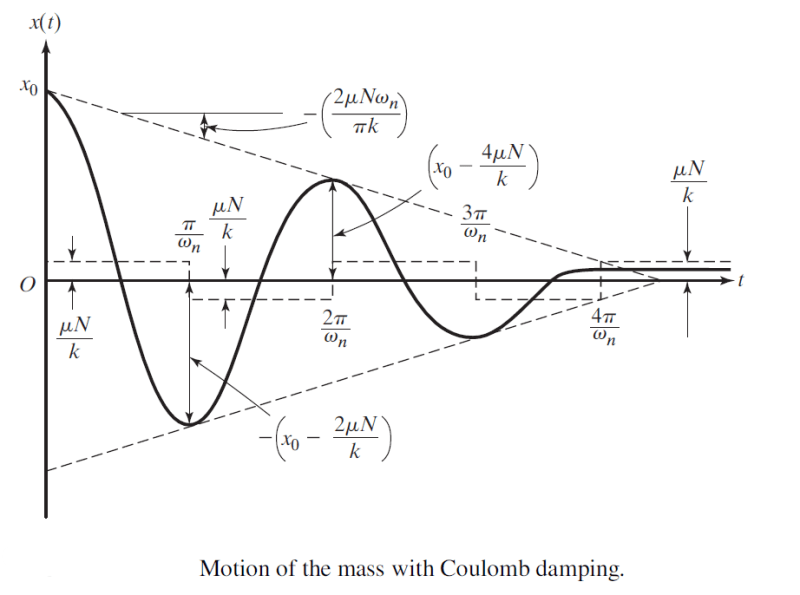
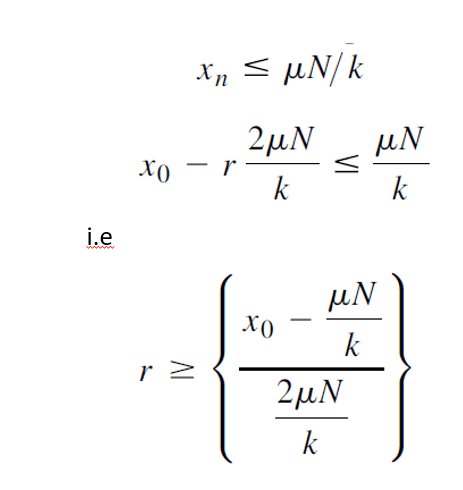
"r" is the number of half cycles that elapse before motion ceases. However, the equation assumes a spring participates in the situation (hence the variable "k"). It also assumes there is an initial displacement, x0 applied to the assembly. Neither the spring, nor the initial displacement occur in my scenario. Does anyone know how or if Coulomb's equation is modified to account for my scenario?
(note: yes, I understand an imbalance in the rotating assembly is likely the cause of the vibration and should be looked at. However, for all intents and purposes, we can assume in this conversation that the source of the vibration is there to stay. The structure and its motor are huge. So even a tiny imbalance may lead to large energy addition to the structure. With a free DOF along the skids, the energy may be enough to excite movement.)

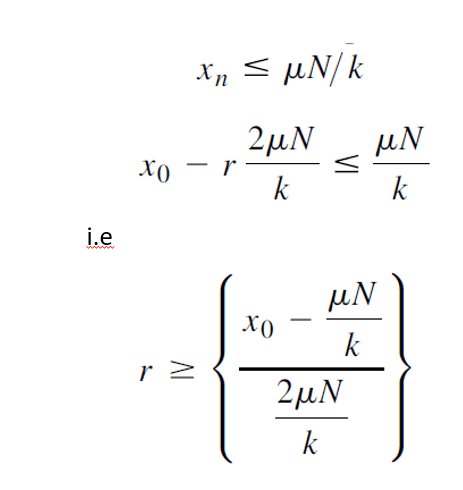
"r" is the number of half cycles that elapse before motion ceases. However, the equation assumes a spring participates in the situation (hence the variable "k"). It also assumes there is an initial displacement, x0 applied to the assembly. Neither the spring, nor the initial displacement occur in my scenario. Does anyone know how or if Coulomb's equation is modified to account for my scenario?
(note: yes, I understand an imbalance in the rotating assembly is likely the cause of the vibration and should be looked at. However, for all intents and purposes, we can assume in this conversation that the source of the vibration is there to stay. The structure and its motor are huge. So even a tiny imbalance may lead to large energy addition to the structure. With a free DOF along the skids, the energy may be enough to excite movement.)
