TEIF-RO
Mechanical
- Apr 1, 2019
- 21
Hi
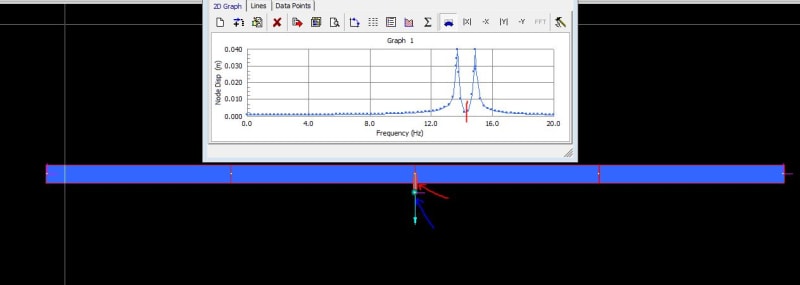
I want to mount a TMD (m,k,c) on my beam-like structure in Abaqus. The beam has a mass at its top(point mass in abaqus). Practically, a tmd should be placed inside the top mass. Its seems impossible to do this as the top mass here is a point!!!
Should a TMD mass be also a point mass?
if yes how to connect spring and dashpot on it?
if not what can be the best choice?
Thanks!
I want to mount a TMD (m,k,c) on my beam-like structure in Abaqus. The beam has a mass at its top(point mass in abaqus). Practically, a tmd should be placed inside the top mass. Its seems impossible to do this as the top mass here is a point!!!
Should a TMD mass be also a point mass?
if yes how to connect spring and dashpot on it?
if not what can be the best choice?
Thanks!