Hi,
I'm looking to understand how to analyze a low speed (100s of RPM) rotating shaft system. It has two radial bearings, one thrust bearing, and two rotors. I'm doing background reading to understand what a critical speed is, and I'm getting confused about how to go from analyzing a shaft in the stationary, non-rotating reference frame to the rotating frame. If I analyze the system without any rotation, I can get the torsional and lateral natural frequencies for the shaft just by doing a hand calculation or running a static eigenvalue FEA (SOL103). For example, this formula appears to provide the torsional frequencies:
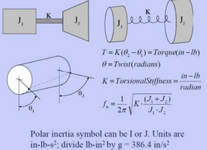
However, in reading about critical speeds of shaft, the first critical speed for a simple system looks the same as the first lateral natural frequency mode shape. Am I right in thinking that gyroscopic and centrifugal forces seem to influence the lateral natural frequencies of the shaft in the rotating reference, as they essentially provide a "stiffening" effect in the rotating frame, and therefore I can't use a simple eigenvalue FEA to evaluate frequencies of concern? Are these first and second critical speeds the same as the 1st and 2nd natural bending frequencies in the static frame, or are they separate modes that require a mass unbalance to calculate and occur?
Any resources would be greatly appreciated, thank you. I haven't had much exposure to dynamic vibration analysis before. I see a lot of resources presenting the case of an off-center mass on a stiff shaft, but I'm more looking to see whether the modes calculated in the static reference frame have any bearing on the modes of the same shaft system when it is rotating at a given speed, even for a hypothetically perfectly balanced system about the rotational axis.
I'm looking to understand how to analyze a low speed (100s of RPM) rotating shaft system. It has two radial bearings, one thrust bearing, and two rotors. I'm doing background reading to understand what a critical speed is, and I'm getting confused about how to go from analyzing a shaft in the stationary, non-rotating reference frame to the rotating frame. If I analyze the system without any rotation, I can get the torsional and lateral natural frequencies for the shaft just by doing a hand calculation or running a static eigenvalue FEA (SOL103). For example, this formula appears to provide the torsional frequencies:

However, in reading about critical speeds of shaft, the first critical speed for a simple system looks the same as the first lateral natural frequency mode shape. Am I right in thinking that gyroscopic and centrifugal forces seem to influence the lateral natural frequencies of the shaft in the rotating reference, as they essentially provide a "stiffening" effect in the rotating frame, and therefore I can't use a simple eigenvalue FEA to evaluate frequencies of concern? Are these first and second critical speeds the same as the 1st and 2nd natural bending frequencies in the static frame, or are they separate modes that require a mass unbalance to calculate and occur?
Any resources would be greatly appreciated, thank you. I haven't had much exposure to dynamic vibration analysis before. I see a lot of resources presenting the case of an off-center mass on a stiff shaft, but I'm more looking to see whether the modes calculated in the static reference frame have any bearing on the modes of the same shaft system when it is rotating at a given speed, even for a hypothetically perfectly balanced system about the rotational axis.
