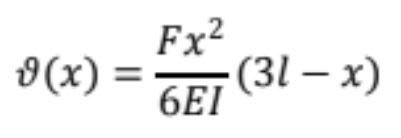Amine A
Mechanical
- May 9, 2020
- 80
Hello community,
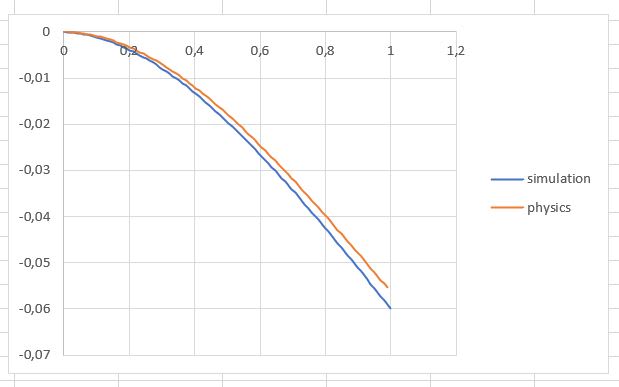
I want to formulate a data-driven calibration model between physics and simulation results. I have an a model encapsulated in an executable program (data_generator.py) that for a load 𝑃 located at 𝑦 = 𝐿, generate 𝑁𝐵 random beam widths 𝑏(𝑥) and computed the beam displacement 𝑤(𝑥) at 𝑁 positions, at locations 𝑥(𝑖) = (𝑖 − 1) ⋅ 𝐿/(𝑁 − 1) ( file attached shows the beam )
I run the two cases (simulation results 'case 1' and physical model 'case 0')
Usage: data_generator.py <case> ...
* Case 0: Physical model
Usage: data_generator.py 0 <L> <h> <b> <P> <N> <y>
- L: Beam length (default 1)
- h: Beam height (default 0.01)
- b: Beam width (default 0.01)
- P: Load (default 30)
- N: Number of steps (default 100)
- y: Position to apply load on beam (default equal to L)
* Case 1: Simulation results
Usage: data_generator.py 1 <L> <h> <b> <P> <N> <y>
- L: Beam length (default 1)
- h: Beam height (default 0.01)
- b: Beam width (default 0.01)
- P: Load (default 30)
- N: Number of steps (default 100)
- y: Position to apply load on beam (default equal to L)
it gives me results in file attached. I don't know how to proceed to do a data-driven calibration model. anyone has an idea please ?
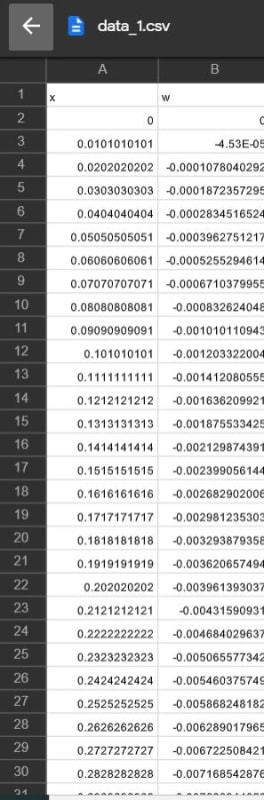
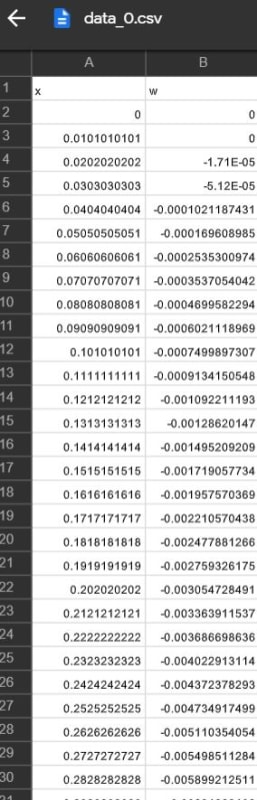
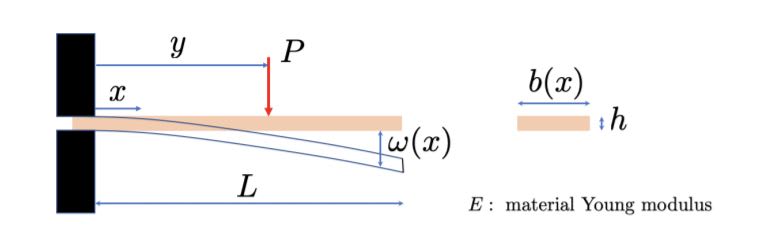
I want to formulate a data-driven calibration model between physics and simulation results. I have an a model encapsulated in an executable program (data_generator.py) that for a load 𝑃 located at 𝑦 = 𝐿, generate 𝑁𝐵 random beam widths 𝑏(𝑥) and computed the beam displacement 𝑤(𝑥) at 𝑁 positions, at locations 𝑥(𝑖) = (𝑖 − 1) ⋅ 𝐿/(𝑁 − 1) ( file attached shows the beam )
I run the two cases (simulation results 'case 1' and physical model 'case 0')
Usage: data_generator.py <case> ...
* Case 0: Physical model
Usage: data_generator.py 0 <L> <h> <b> <P> <N> <y>
- L: Beam length (default 1)
- h: Beam height (default 0.01)
- b: Beam width (default 0.01)
- P: Load (default 30)
- N: Number of steps (default 100)
- y: Position to apply load on beam (default equal to L)
* Case 1: Simulation results
Usage: data_generator.py 1 <L> <h> <b> <P> <N> <y>
- L: Beam length (default 1)
- h: Beam height (default 0.01)
- b: Beam width (default 0.01)
- P: Load (default 30)
- N: Number of steps (default 100)
- y: Position to apply load on beam (default equal to L)
it gives me results in file attached. I don't know how to proceed to do a data-driven calibration model. anyone has an idea please ?




![[dazed] [dazed] [dazed]](/data/assets/smilies/dazed.gif)
![[smile] [smile] [smile]](/data/assets/smilies/smile.gif) I will try to see if the "m" and "b" should be a function of parameters given in the problem (shown in figures below)
I will try to see if the "m" and "b" should be a function of parameters given in the problem (shown in figures below)

![[hourglass] [hourglass] [hourglass]](/data/assets/smilies/hourglass.gif)