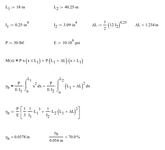Deflection of two beams 90deg apart

[fortjp500]

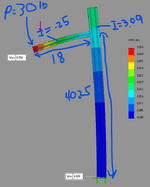
Good morning, I'm struggling to find the theory of how to validate the deflection of two pieces of 8020 aluminum extrusion that are assumed to be fixed to each other and fixed to the ground. I think I'm going about it wrong, but when I calculate the static beam deflection of a point load applied to the end of the smaller piece and then calculate the static deflection of the vertical post from the moment that is being applied I can't get to the FEA result.

 

[fortjp500]

Here's some info if the details help.

 

[3DDave]

The vertical beam is subject to a constant bending moment/couple at the end. The horizontal one is subject to a linearly applied bending moment.

There will also be a probably tiny amount of linear compression of the vertical beam and a tiny amount of shear deflection of the horizontal one, but those are usually negligible in comparison to bending.

Most any book on beam deflection will have formulas for them both.

Search for beam deflection formula

 

[fortjp500]

The vertical beam is subject to a constant bending moment/couple at the end. The horizontal one is subject to a linearly applied bending moment.

There will also be a probably tiny amount of linear compression of the vertical beam and a tiny amount of shear deflection of the horizontal one, but those are usually negligible in comparison to bending.

Most any book on beam deflection will have formulas for them both.

Search for beam deflection formula

Yeah I have both of those calculated but would you just add those together? The result of that is much less than what FEA is giving for displacement.

 

[Stick.]

When you're adding together the two component deflections (one for horizontal beam and one for vertical beam), are you also accounting for the rotation of the interface between the two? The slope/rotation of the vertical beam at the connection will translate into a rotation of the whole horizontal beam, on top of the deflection within that horizontal beam itself.

 

[fortjp500]

When you're adding together the two component deflections (one for horizontal beam and one for vertical beam), are you also accounting for the rotation of the interface between the two? The slope/rotation of the vertical beam at the connection will translate into a rotation of the whole horizontal beam, on top of the deflection within that horizontal beam itself.

I was not. I think that will likely be the factor I'm missing. Thanks.

 

[fortjp500]

I was not. I think that will likely be the factor I'm missing. Thanks.

I'm not 100% on how to determine what that rotation of the interface will be. Can I just look at the inverse tangent of the vertical's deflection from the moment over the vertical's length to get an angle to apply to the horizontal?

 

[3DDave]

See the fifth figure: https://civilengineerspk.com/wp-content/uploads/2014/05/1399860224-Beamdeflec-o.jpg

 

[fortjp500]

See the fifth figure: https://civilengineerspk.com/wp-content/uploads/2014/05/1399860224-Beamdeflec-o.jpg

Thanks for that. Those interface angle equations are very useful. But in my case of the vertical aluminum extrusion interface angle ends up being 0.0007° which results in only .0002" of deflection from interface rotation and the 18" horizontal member rotating prior to it's own deflection. So I'm still stumped why I can't match the FEA deflection.

 

[3DDave]

The result is in radians, not degrees, so ~0.045º.

So 0.0007*18 = .0126 inches added to the bending of the horizontal beam, or 25% of the answer from the FEA on vertical beam bending alone.

 

[fortjp500]

The result is in radians, not degrees, so ~0.045º.

So 0.0007*18 = .0126 inches added to the bending of the horizontal beam, or 25% of the answer from the FEA on vertical beam bending alone.

Thanks that gets me close enough.

 

[Stress_Eng]

I think this is part of the way to calculating the total deflection. This is just for bending, the horizontal beam will also have shear deflection and the vertical will have a compression displacement (section areas, E and G needed). 'Delta L' is 1/2 of the vertical column width.