Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
If you neglect the friction , you may assume one third the deflection of one plate as Compositepro stated.How do you calculate the deflection of three unbonded layers of steel plates with a middle point load ?

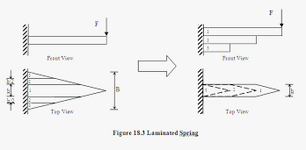
That is what I would assume.It will be one third the deflection of one plate.
The devil is in the loading from zero, once all the plates are firmly in contact then the 1/3 calculation is correct.
Isn't this a first year mechanics of materials question?
