Dimensions Calculation for a "Pyramid" Inside a Rectangle (Terrarium Setup) 3

[SnailBait]

Good day!

I do not work in engineering but i am a librarian with a new passion to terrariums.

I would need some advice for calculating the measurements for the sides of a flat top pyramid inside a rectangular terrarium.

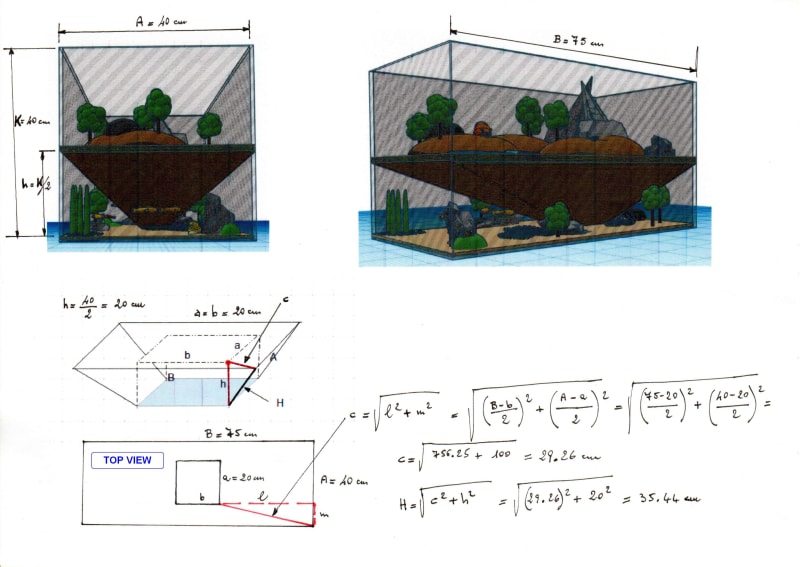
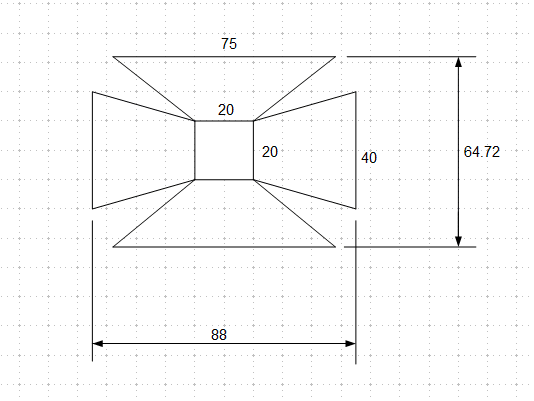
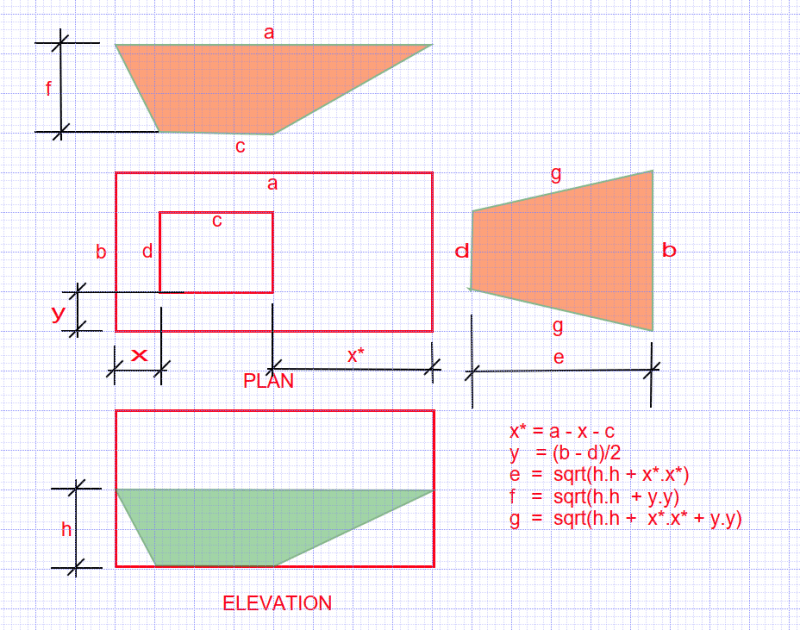
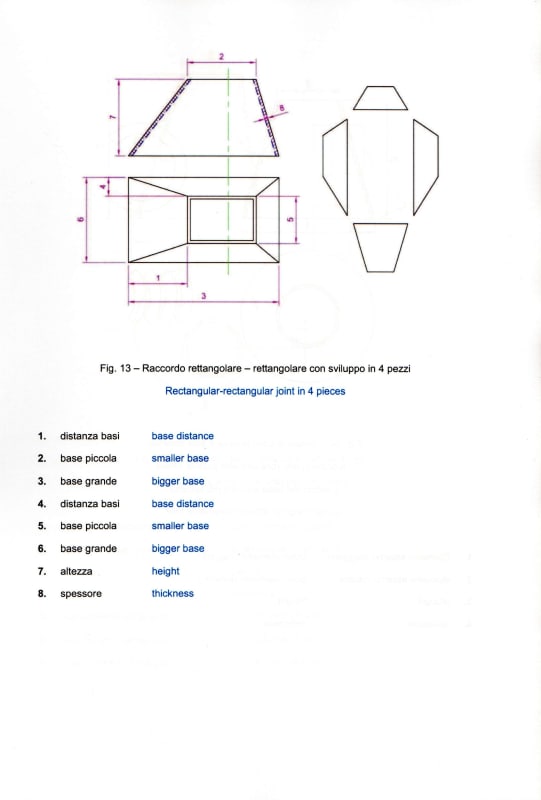
Added is some screenshots of my 3D-model to show what im working with. The terrarium is 75x40x40cm and the square at the bottom of the pyramid will be 15x15cm or 20x20cm.

So what im doing is im building a 2 level aquarium/terrarium. Bottom level will be filled with water and the levels divided by a "flat top pyramid" shape made out of plexiglass/polycarbon sheet 3mm thick.

Because the pyramid is upside down and i need some sort of structural integrity for it to be stable i decided to level it (will have a pump inside it too).

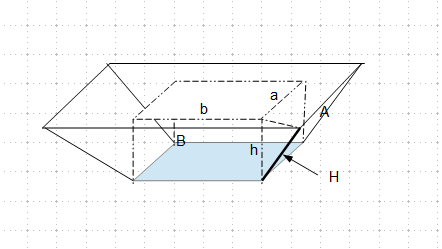
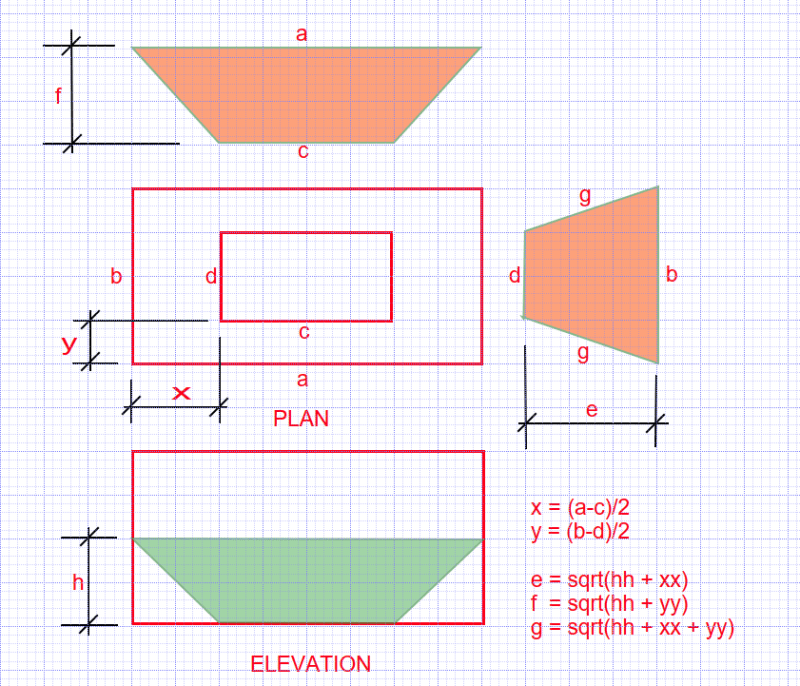
My problem and question is. What is the method/formula to get outside measurements of the four separate pyramid walls? "The terrarium is 75x40x40cm and the square at the bottom of the pyramid will be 15x15cm or 20x20cm."

Might be something obvious im just not realizing but i tried to search online for information but english isnt my first language and im not sure what terms to use for finding my answer.

So this is why i figured an engineering forum might be my best chance!

Thank you in advance!

 

[SnailBait]

Heres another image.

 

[JLNJ]

Shouldn’t be too hard. Just apply the Pythagorean theorem. The one thing missing is the distance up from the bottom to the base of the pyramid at the top.

Also, do you want it to be symmetrical? It looks offset in your sketch.

 

[BAretired]

The shape you are describing is a truncated square pyramid. With height h, dimension a, b the square dimension at bottom and top respectively, the sloping dimension of each side can be found using Pythagoras' theorem.

Let c = (a-b)/2

then h' = (h²+c²)^0.5

EDIT: If a = 40, b = 20 and h = 75/2 = 37.5,
then c = (40 - 20)/2 = 10
and sloping height h' = (10² + 37.5²)^0.5 = 39.1


BA

 

[SnTMan]

SnailBait, if you have modeled the thing, how do you not have dimensions? BTW, probably more suited to the Hobbies forum.

Regards,

Mike

The problem with sloppy work is that the supply FAR EXCEEDS the demand

 

[dik]

RTFM is not an answer and is of little help... thanks BART.


BART may not hang out there...

Dik

 

[SnTMan]

Hmmm, something gone missing here?

The problem with sloppy work is that the supply FAR EXCEEDS the demand

 

[r13]

dik,

Isn't this all geometry and trigonometry?

 

[BAretired]

H = (h² + 2c²)^1/2

For a, b, h = 40, 20, 37.5 respectively,
c = 10; H = 40.08 (edge shown in retired13's sketch)
h' is the actual width of plexiglass required for each wall.

N.B. For a good fit, plexiglass edges must be cut to the proper angle.




BA

 

[robyengIT]

 

[SnailBait]

A quick thank you to all of you who have responded. Amazed to see so many replies in such a short time.

Don't have time to check everything now, going picking mushrooms. But I will do so later and respond better then!

 

[SnailBait]

JLNJ - I'm going to have one side longer because of the mountain which is placed on top of the square bottom.

For the hight im thinking eighter 12 or 14cm not 100% sure yet.

SnTMan - I do have general dimensions but I used Tinkercad to model it and I didn't figure out how to get measurements of the angled parts. It doesn't show them automatically and the ruler tool didn't work as I thought it would.

Thank you all for the pictures and drawings! This should really get me started!

Will see how well I get the plexiglass edges fixed. I'm working with limited tools. Ruler, boxcutter and hand held electric belt sander. Shouldn't be a problem!

 

[r13]

Cut a cardboard to verify dimensions before ordering material.

 

[BAretired]

Looks like I misinterpreted the dimensions. Using the dimensions of robyengIT, I agree with his calculation of 'H', the diagonal edge of the terrarium, but that is not the dimension needed to order the material.

Below is a plan and elevation of the terrarium. The truncated rectangular pyramid is shown in green. The plexiglass wall dimensions are shown in orange.

Note: sqrt means square root.
EDIT: Corrected errors in sketch

BA

 

[JLNJ]

I don’t believe it is as symmetrical as you all think. It’s a loo-sides pyramid.

Got to think like an artist, not a structural engineer.

 

[r13]

JLNJ,

When one has grabbed the fundamental, no mater how it is shaped, just follow the basics. Straight lines, no curve though.

 

[JLNJ]

When one doesn’t understand the question, there is no point in giving a detailed answer.

 

[r13]

Then you shall demonstrate your understanding and provide the perceived correct solution. This is the purpose of this forum - to discuss and exchange ideas.

 

[BAretired]

Just getting a feel for a loo-sided pyramid.
Might be fun to make the tank a trapezoid, rhombus or irregular pentagon.

BA

 

[robyengIT]

During my job I was using a program to unfold steel sheet : very easy and quick to have result. I am available to give solution (as many time you like, question of 1 minute) according to the attached scheme