Direct Analysis - ACI 318 3

[vishalselvan]

Hello everyone,

I am trying to analyze a building that has both steel framing for the first few floors and is then continued upwards as a concrete structure. I was able to use AISC's direct analysis method to check the deflections in the steel framing and check the members for strength using reduced EI properties.

When I get to checking concrete, the code doesn't give an explicit method on how to do something similar to that shown in AISC. My understanding is that I can use moment magnifiers or run the analysis with P-delta turned on. My goal is to analyze the entire model in one fashion, and I'm interested in finding out how to analyse the concrete structure with P-delta.

1) Would sway/non-sway not matter when P-delta analysis is done? In AISC, they mention that k=1 in P-delta analysis.

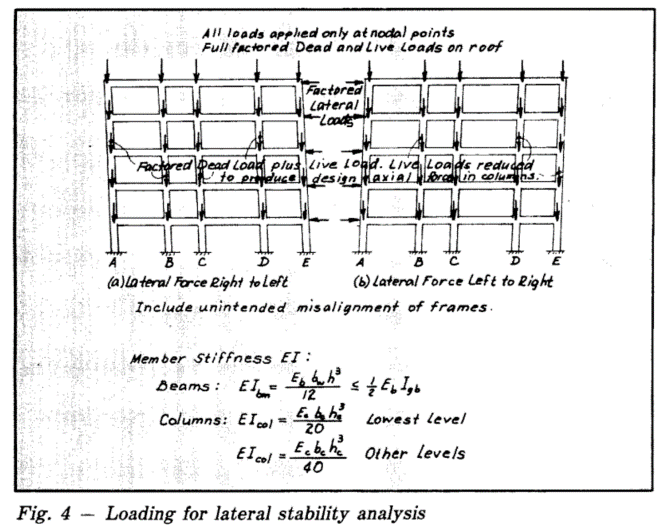
2) Is there an equivalent for the iterative method to find EI for steel for applying to concrete? I found that the material non-linearity is accounted for in Table 6.6.3.1.1 (c) (ACI 318-14). I am not sure if there is another reduction that I need to apply.

I'm using RISA 3D to perform the analysis. I would appreciate any help as I do not have a lot of experience in dealing with concrete structures.

Thanks,

Vishal

 

[JoshPlumSE]

This is one of my favorite topics.....

Some generalized thoughts that might help:

a) Why are you allowed to use K=1.0 when using the AISC direct analysis method. This is because:
- You have accounted for initial imperfections (which is in the column equations) and out-of-plumbness (notional loads).
- You have included both P-Big Delta and P-little delta in the analysis.
- You have accounted for inelastic material behavior via the use of the Tau_b adjustment factor.

b) In ACI, you have not done all these things.
- Out of plumbness certainly isn't accounted for. Though member imperfections are sort of.... via the use of some minimum moments.
- Your P-Delta analysis has probably accounted for P-Big Delta, but RISA does not account for the little delta effect. Though you can do so by subdividing your columns or use the moment magnification methods on individual members.
- Material non-linearity isn't really accounted for. Though it's not clear to me what kind of buckling concrete columns or frames experience. Probably not as clean as the steel ones. Therefore, no clean method (that I'm aware of) for adjusting EI values to better capture the buckling of concrete column like you get from AISC's Direct Analysis Method.

c) Because of this, you will often not be able to use K=1.0 for concrete members.

 

[vishalselvan]

Hello Josh,

Thank you for replying. I have been reading your thoughts in your other posts regarding this, such as in this thread.

https://www.eng-tips.com/viewthread.cfm?qid=416199

Assuming b-1,b-2 are taken care of using a similar notional load and we subdivide the columns to get P-delta working, I'm still confused as to how to perform the analysis or check using Risa or an equivalent while accounting for all the points you mentioned. Would you say it is then dependent on judgement with the risk of being overly and unrealistically conservative?

I'm checking an existing building having a steel framing for a few floors which then support concrete framing for 30 floors, for additional loads imposed on it due to alterations and changes made in it. These changes are major ones such as removal of shear walls. So we figured that the best thing to do would be to try and fit concrete into the DAM used for AISC but it seems challenging.

 

[JoshPlumSE]

There is one thing that I left unsaid that is probably pretty important..... The requirements of the concrete analysis and the steel analysis do NOT necessarily match up. Therefore, you MAY have to do two separate analyses of your structure:

1) Perform an AISC Direct Analysis Method type of analysis where you use RISA's P-Delta analysis (with subdivided columns to capture the little delta effect) including whatever notional loads are required. You would manually adjust concrete stiffness (using the I_crack factors) per the AISC design guide 28 recommendations. This is all to comply with the AISC direct analysis method and will be used to perform your code checks on the steel members.

Note: Can you use this to perform the code checks on the concrete members too? That's a matter of engineering judgement. I'd say that you can. This isn't really trying to capture the true behavior.... Just good enough behavior to get acceptable forces and moments for design. The real behavior is much more non-linear than we can afford to do on a real design project. That being said, I would still use the K factors for concrete columns because there I'm not sure there is a good code basis for dropping this to 1.0 like you do for the steel members.

2) If you decide that you CANNOT use the concrete forces and moments from the 1st analysis, then you need to perform a 2nd analysis based off of ONLY the analysis requirements of the ACI codes. Meaning you ignore the Direct Analysis method adjustments and only adjust the stiffness of concrete members for cracking. This would still invoke RISA's P-Delta analysis (with column subdivision to capture the p-little delta effect).
Note: Technically the subdivision of columns is only allowed by newer versions (ACI 2008 and newer?). If you're using an older version, your process in RISA would be a little bit different.

 

[Settingsun]

Not official documents, but Richard Furlong's papers about 'rational analysis' of concrete frames probably provide what you need. I'd divide his stiffnesses by (1+Beta,d) to account for creep. And he does recommend a final check of slender sway columns using the procedure for braced columns.

 

[vishalselvan]

Thank you so much Josh and steveh, this will help me immensely to get a grip on analyzing concrete frames!!

 

[KootK]

1) I feel that we need some additional information in order to provide you with the best possible advice vishalselvan:

a) How has it come to pass that you'll be building a bunch of concrete floors over steel framed floors? I've never heard of this being done and it bespeaks some potentially serious seismic irregularity if your project will be constructed in a seismic environment. Concrete over steel is strange enough of a decision that I feel we need to understand the reasoning for it.

b) What is the existing building lateral system? Shear walls alone?

c) What will be the designated lateral system(s) after you alterations? Frankly, if your designated lateral system remains shear walls alone, there I'm not sure there's a need to get into the direct design method approach as that is really meant for flexible systems such as moment frames. Conversely, if you're stacking 30 stories of heavy concrete over top of steel moment framed levels at the base, I question whether that's even a wise design approach to begin with.

My take on your specific questions follows:

Would sway/non-sway not matter when P-delta analysis is done? In AISC, they mention that k=1 in P-delta analysis.

2) Your assertion is correct and the procedure would be as follows, with reference to ACI 318-14:

a) 6.6.4.6.2.c: Determine your column end moments, magnified for sway, via second order analysis (P-Big-Delta).

b) 6.6.4.6.4: Proceed to 6.6.4.5, the non-sway moment magnification method, modifying that procedure only by calculating Cm using the amplified moments from step #a (P-Little-Delta)

c) 6.6.4.5.2: At long last, you're using K to determine Pc. You are doing so, however, within the context a non-sway problem per step #b. And, per 6.6.4.4.3, K<=1 for non-sway problems.

So, in reality, ACI had this K=1 business nailed down long before AISC started kicking up a fuss.

I know, it would be nicer if ACI said something like this in 6.6.4.6.4: Go forth and amplify your moments per the non-sway procedure with Cm calculated with the second order moments and K=1! I take the latter part of that statement to be implied however for two reasons:

d) K=1 makes sense here for the same reasons that it does for AISC DAM. Namely, the sway aspect of instability has already been taken care of by the second order analysis and it would be double dipping to account for it again when looking at moment amplification between the ends of the member.

e) The last paragraph of 6.6.4.6.2 specifically tells you to calculate Pc using the K-factor for sway members when using option (b). So, when they mean for you to use K>1 for Pc, it seems that they make of point of saying so.

2) Is there an equivalent for the iterative method to find EI for steel for applying to concrete? I found that the material non-linearity is accounted for in Table 6.6.3.1.1 (c) (ACI 318-14). I am not sure if there is another reduction that I need to apply.

I think that tables 6.6.3.1.1 A & B are just the way to go with no additional reductions required.

So we figured that the best thing to do would be to try and fit concrete into the DAM used for AISC but it seems challenging.

3) I think that procedure would be both appropriate and doable as follows:

a) Apply notional loads to levels, steel and concrete, in a whole building model.

b) Make the modifications to the steel famed levels per AISC DAM.

c) Run your model as non-linear P-Delta.

d) Design your concrete levels per section #2 above.

e) Design your steel levels per the usual AISC DAM methods.

I can't see any way in which this would violate the tenets of either AISC or ACI design.


HELP! I'd like your help with a thread that I was forced to move to the business issues section where it will surely be seen by next to nobody that matters to me:

http://www.eng-tips.com/viewthread.cfm?qid=456235

 

[Settingsun]

KootK,
Thanks for that. I don't use ACI but looked up those clauses to follow along at home. In step 2c, is it 6.6.4.5.2 instead of 6.6.4.2? And option b instead of option d in step 2c2 (referring to 6.6.4.6.2)?

I know, it would be nicer if ACI said something like this in 6.6.4.6.4: Go forth and amplify your moments per the non-sway procedure with Cm calculated with the second order moments and K=1!

Or use the 's' and 'ns' subscripts eg Pc,ns for K<=1.

So, in reality, ACI had this K=1 business nailed down long before AISC started kicking up a fuss.]

One of the Furlong papers I referred to is from 1981. When I found out about AISC's DAM this year (pretty filthy I didn't know sooner...), I immediately thought it's Furlong's method but for steel.

I like this from the 1981 paper:

The ACI Building Code, Clause 10.11.6, regarding moment magnification factors for columns in unbraced frames may have yet to be applied completely and correctly in the design of an entire concrete structure.

I gather he wasn't a fan. Is UTA a 'big' structural university?

 

[KootK]

Thanks for that. I don't use ACI but looked up those clauses to follow along at home. In step 2c, is it 6.6.4.5.2 instead of 6.6.4.2? And option b instead of option d in step 2c2 (referring to 6.6.4.6.2)?

You're right on both counts. I've updated my blurb accordingly. And you're most welcome. I often feel a little foolish wasting precious weekend/family time writing this stuff up, plagued by a sneaking suspicion that nobody will actually bother to read it. But, clearly, you read it. So thanks for that.

Is UTA a 'big' structural university?

Oh yeah. My impression is that they get a lot of research funding for bridge related work from the US Federal Highway administration. As a result, they've done a done of great stuff within the realms of strut and tie research and structural steel stability (Yura was there).

Can you supply the titles of the Furlong papers that you feel are germane to this discussion? I'd like to get my hands on what you've seen on this, at least the freebies. So far, this is the only freebie that I've found: Link

I gather he wasn't a fan.

It doesn't seem like it does it? In terms of accuracy, efficiency, and modernity, there's little doubt hat we're headed towards DAM and away from K-factor/bifurcation. And I support that given the tools that are now available to us. That said:

1) The K-factor method was/is seriously elegant. When you consider the scale of what that relatively simple method captured, somewhat reasonably, it's mind boggling. Galambos recently published a book on stability that includes a nifty appendix showing the derivation of the effective length method. Frankly, I didn't fully understand or appreciate the method until I read that. DAM is an improvement for all of the usual reasons but, in my opinion, it's nowhere near as element as the effective length method. DAM is basically just brute force computing after all.

2) My understanding is that DAM can greatly improve structural efficiency compared to the effective length method. Just looking at slender concrete columns in isolation, a second order treatment can easily reduce moment magnification by a factor of five relative to the traditional approach. That's great but it makes one wonder if designers will be more likely to get themselves into trouble with these new methods. Our profession, on average, has never been great at stability in my opinion. I suspect that many possible problems have, in the past, been averted due to the conservatism in our methods for evaluating stability. You know the drill with engineering: we push and push until nature gives us a reason to pull back.



HELP! I'd like your help with a thread that I was forced to move to the business issues section where it will surely be seen by next to nobody that matters to me:

http://www.eng-tips.com/viewthread.cfm?qid=456235

 

[Settingsun]

I'm not sure you'd (KootK) find much new material in the Furlong papers as it seems you're across the basis and practical requirements. The two I have are:

"Rational Analysis of Multistory Concrete Structures" (Concrete International, June 1981); and

"Elastic Rational Analysis and Tests of Unbraced Concrete Frames (in the book/proceedings 'Progress in Structural Engineering, 1991)

The 1981 paper shows its age by describing how to iterate manually so that a first-order-only analysis program can be used for p-DELTA effects (manually increase the nominal lateral loads after each analysis). Its member stiffness recommendations are superseded by ACI318. The remaining bit of interest is how he handles the differing area reduction of live load for sway effects (large tributary areas based on several storeys) and gravity pattern loading (small tributary area based on individual beams). See Figure 4 below - the gravity loads for sway analysis (maximum area reduction) are applied at nodes so this analysis only gives moments and shears for sway effects. You then add the worst-case effects for loading on beam spans (pattern loads with small area reduction).

The 1991 paper has updated stiffness recommendations (also superseded now) but also a proposed addtional reduction factor for frames with few columns. For two columns, the reduction factor is 0.66 so you analyse a lower-bound frame stiffness (dodgy concrete). For >10 columns, the factor is 0.9 (just a notional reduction of average stiffness) as that many columns should even our the frame stiffness to the value for 'average' concrete.

The K-factor method was/is seriously elegant.

The shortcoming as I understand it was that the evaluation of K relies on pretty gross assumptions. I watched an AISC video where the presenter (R. Shankar Nair, chairman of AISC Committee 10 on stability) said something like "I don't know how other engineers are calculating K accurately; I certainly don't know how to." Regardless, I imagine that the derivation would be quite enlightening as it probably states where the method is simplified. And the method works, as you said.

 

[Settingsun]

My understanding is that DAM can greatly improve structural efficiency compared to the effective length method. Just looking at slender concrete columns in isolation, a second order treatment can easily reduce moment magnification by a factor of five relative to the traditional approach.

An anecdote from when I was young. I'd been pumping out wharf desgns for a couple of years using second order analysis as I was taught by senior engineers at my first job and had a feel for how big the columns (piles) should be. Then I independently reviewed another consultant's design. The review scope was go through their calculations and make comments, not to do my own calcs. They'd done first-order analysis and I commented that they therefore needed to do monent magnification (which I'd never done for this type of structure). I expected them to come back and say no changes necessary as everything looked about the right size to me. Instead, the entire drawing set was resubmitted three days later with double the number of piles under the crane beam (halving their axial load). It was now ridiculously over-designed and I was passing bricks that it would be blamed on me (my client was paying for construction after all). Built that way AFAIK.

About a year later, one of our designs was being reviewed (by a different consultant than the case above). They'd done their own calcs: first order plus moment magnifiers, and found our design was inadequate. My director had meetings with them about several comments and they'd brought along a textbook to support their view on another matter. My director found in that book a statement that the moment magnifiers are conservative for structures of our proportions and loadings and a recommendation to use second-order analysis instead. The author must have been a giant of engineering in India because the reviewers basically closed the comment on the spot. If Professor Suchandsuch says so, it must be correct.

 

[sticksandtriangles]

A good article on this:

https://www.structuremag.org/?p=1005

I like this quote on the conservative nature of moment magnification:

Simply put, moments estimated by the moment magnification procedure may be upwards of five times larger than those estimated by a second order analysis. As a result, engineers often discount the moment magnification procedure in favor of the more manageable results obtained from an elastic second order analysis. But the question remains, “Why is there such a large difference within the provisions?”

I did my own example with a tall slender concrete wall and got a difference in the range 4.0 of moment magnification vs 2nd order analysis.

S&T

 

[KootK]

One thing I'm curious about is how designers of the future will "design" lateral frames. DAM is great but that's analysis. Will folks just dive into that and swap out members until it works? It almost seems like you'd need something like K-factor in your back pocket to do your preliminary and make an estimate of how to make a failing system work. Maybe one just comes at it with a reasonable, linear elastic drift target or something.

HELP! I'd like your help with a thread that I was forced to move to the business issues section where it will surely be seen by next to nobody that matters to me:

http://www.eng-tips.com/viewthread.cfm?qid=456235

 

[JoshPlumSE]

To me, the reason why DA Method works is because we've got a really, really good idea of the elastic stiffness of steel members. Therefore, if we add in 2nd order effects (geometrically inelastic, but materially elastic) then we add in another adjustment factor to approximate inelastic buckling (based on axial force in the member) then we can get a pretty darned good estimate of the inelastic behavior of the steel structure.

For concrete that's just not true. We generally base our elastic stiffness on the gross concrete moment of inertia... ignoring the effect of reinforcement on the moment of inertia. Then we choose a fairly arbitrary factor for cracking. So, we start off with a much worse starting point. If our starting point isn't very good, then are we really capturing the geometric non-linearity accurately? It's not totally inaccurate, but it's not like it is for steel.

In my opinion, if we were go do a better job with concrete analysis then we'd have to really start with a better moment of inertia. Maybe by adjusting the moment of inertia based on cracking and axial forces and such.... Not sure if I'd go so far as saying that we'd have to do a different moment of inertia for every load case. But, if we decide that the axial force is critical to capturing the buckling, then yes, we probably should use a different moment of inertia for every load case.

 

[Settingsun]

The issue with unpredictable stiffness of concrete elements would have a similar impact under effective length methods. EI is a key input however your work with buckling. With concrete, we need to use a lower bound to the stiffness which is currently achievable. Improving the methods of predicting the stiffness will improve our prediction of average stiffness but 'identical' test specimens can have large difference in stiffness (short & long term). If it can't be controlled in the lab, it won't be on site and we need to be safe.

For steel, I understand that the AISC code has a single 'column curve' for buckling. Australia/NZ have five (AISC is similar to our second strongest) and I think Eurocode also has five depending on expected residual stresses. So the inelastic reduction factor is a rough approximation, or rather only correct for certain fabrication methods.

 

[Agent666]

The shortcoming as I understand it was that the evaluation of K relies on pretty gross assumptions

If you look in AISC, there is a good list of these assumptions and to be fair it's pretty hard to satisfy all of them all of the time as they note with respect to real structures (see appendix 7.2). Reality is most people only relate K back to one of the standard fundamental cases typically outlined in tables (pin/pin, pin/fixed,.. Etc etc).

If you actually use the alignment charts based on stiffness of connecting elements you'll get a more accurate theoretical approximation, but not too many people seem to understand these to be fair based on my experience.

So DAM sort of is a fairly easily understood method to directly allow for stability, certainly for those who love to shove rubbish into a computer without understanding the theories it seems to be a good method as its very visual. You can see what's going on which helps foster understanding of the underlying behaviour when compared to sometimes randomly factoring up moments by some large multiplier you calculated in mysterious ways to allow for some unseen stability effect.

In terms of concrete because I'm dealing with seismic, it's very unusual that you have slender columns in these situations that require moment magnification. P-delta is all that's required if you're over the limits when it requires consideration.