Tygra_1983
Student
- Oct 8, 2021
- 125
Hi all,
I am trying to solve for a gable frame using the Direct Stiffness Method. The frame is obviously constructed of two rafters and two columns. I am quite confused: I am getting the correct results for the columns, but not for the rafters. I am comparing my results to those in ETABS for confirmation of the correct results. I am using my beloved Octave, so I need someone who uses either Octave or MATLAB.
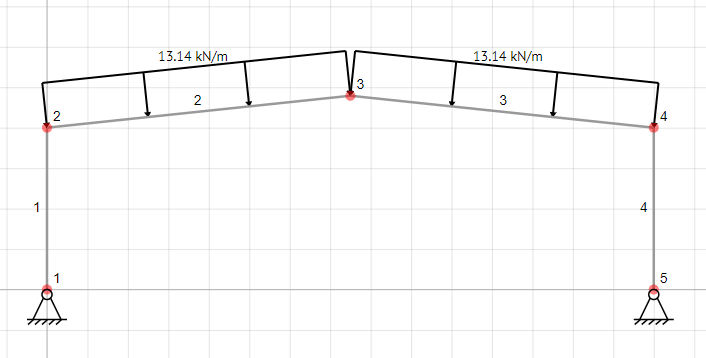
The frame consists of two 8 metre columns, and two 15.083 metre rafters at an angle of 6 degrees to the horizontal. The UDL on the rafters is 13.14 kN/m
Here is the code from Octave:
The force vector gives the axial force, shear and bending moment for a single member over two joints. There are three degress of freedom at each joint.
This is the results for the column:
These results are correct!!
These are the results for the rafter:
These results are incorrect!
I have examined everything and cannot see what is the issue. I know this question is quite time comsuming, so I deeply thank anyone that attempts to help!
I am trying to solve for a gable frame using the Direct Stiffness Method. The frame is obviously constructed of two rafters and two columns. I am quite confused: I am getting the correct results for the columns, but not for the rafters. I am comparing my results to those in ETABS for confirmation of the correct results. I am using my beloved Octave, so I need someone who uses either Octave or MATLAB.
The frame consists of two 8 metre columns, and two 15.083 metre rafters at an angle of 6 degrees to the horizontal. The UDL on the rafters is 13.14 kN/m

Here is the code from Octave:
Code:
clear, clc, close all
[b]% Structural data[/b]
E = 2.1E+08;
Ic = 8.74999E-04; [b]Second Moment areas of Columns[/b]
Ac = 0.01442; [b] Cross-sectional areas of columns[/b]
Lc = 8;
n = 15;
alpha = 6 [b]Slope of roof in degrees[/b]
matrix = zeros(6,n);
Lr = 15/(cosd(alpha))
Ir = 2.94331E-04 [b]Second Moment areas of rafters[/b]
Ar = 0.00856; [b] Cross-sectional areas of rafters[/b]
[b]% Local stiffness matrix for columns[/b]
Kc = [1 0 0 -1 0 0
0 12 6*Lc 0 -12 6*Lc
0 6*Lc 4*Lc^2 0 -6*Lc 2*Lc^2
-1 0 0 1 0 0
0 -12 -6*Lc 0 12 -6*Lc
0 6*Lc 2*Lc^2 0 -6*Lc 4*Lc^2]
[b]% Local stiffness matrix for rafters[/b]
Kr = [1 0 0 -1 0 0
0 12 6*Lr 0 -12 6*Lr
0 6*Lr 4*Lr^2 0 -6*Lr 2*Lr^2
-1 0 0 1 0 0
0 -12 -6*Lr 0 12 -6*Lr
0 6*Lr 2*Lr^2 0 -6*Lr 4*Lr^2]
[b]% For loop to complete the local stiffness matrices[/b]
for i = 1:6
if i == 1 || i == 4
Kc(i,:) = Kc(i,:)*(E*Ac)/Lc;
Kr(i,:) = Kr(i,:)*(E*Ar)/Lr;
else
Kc(i,:) = Kc(i,:)*(E*Ic)/Lc^3;
Kr(i,:) = Kr(i,:)*(E*Ir)/Lr^3;
end
end
[b] % Transformation matrices[/b]
T1 = matrix; [b]For Left Column[/b]
T1(2,1) = -1;
T1(1,2) = 1;
T1(3,3) = 1;
T1(5,4) = -1;
T1(4,5) = 1;
T1(6,6) = 1
T4 = matrix; [b]For right column[/b]
T4(2,13) = -1;
T4(1,14) = 1;
T4(3,15) = 1;
T4(5,10) = -1;
T4(4,11) = 1;
T4(6,12) = 1;
T2 = matrix;
T2(1,4) = cosd(alpha); [b]For left rafter[/b]
T2(1,5) = sind(alpha);
T2(2,4) = -sind(alpha);
T2(2,5) = cosd(alpha);
T2(3,6) = 1;
T2(4,7) = cosd(alpha);
T2(4,8) = sind(alpha);
T2(5,7) = -sind(alpha);
T2(5,8) = cosd(alpha);
T2(6,9) = 1;
T3 = matrix;
T3(1,7) = cosd(-alpha); [b]For right Rafter[/b]
T3(1,8) = sind(-alpha);
T3(2,7) = -sind(-alpha);
T3(2,8) = cosd(-alpha);
T3(3,9) = 1;
T3(4,10) = cosd(-alpha);
T3(4,11) = sind(-alpha);
T3(5,10) = -sind(-alpha);
T3(5,11) = cosd(-alpha);
T3(6,12) = 1;
[b]% Assembly[/b]
km1 = T1'*Kc*T1;
km2 = T2'*Kr*T2;
km3 = T3'*Kr*T3;
km4 = T4'*Kc*T4;
Ks = km1 + km2 + km3 + km4
[b] % Application of boundary conditions[/b]
Ks(:,[1,2,13,14]) =[];
Ks([1,2,13,14],:) =[];
[b]% Applying loading[/b]
w = 13.14;
V = w*Lr/2;
M = w*Lr^2/12;
F = zeros(n,1);
F(4) = -V*sind(alpha);
F(5) = V*cosd(alpha);
F(6) = M;
F(8) = 2*V*cosd(alpha);
F(9) = 0;
F(10) = V*sind(alpha);
F(11) = V*cosd(alpha)
F(12) = -M;
F([1,2,13,14]) = []
[b]% Solving[/b]
U = inv(Ks)*F
Ux = [0 0 U(1:10)' 0 0 U(11)'];
fx = T2*Ux'
force = Kr*fxThe force vector gives the axial force, shear and bending moment for a single member over two joints. There are three degress of freedom at each joint.
This is the results for the column:
Code:
Ux = [0 0 U(1:10)' 0 0 U(11)'];
fx = T1*Ux'
force = Kc*fx
force =
-197.1000
108.3198
0
197.1000
-108.3198
866.5586These results are correct!!
These are the results for the rafter:
Code:
Ux = [0 0 U(1:10)' 0 0 U(11)'];
fx = T2*Ux'
force = Kr*fx
force =
-128.329
-85.605
-617.462
128.329
85.605
-673.685These results are incorrect!
I have examined everything and cannot see what is the issue. I know this question is quite time comsuming, so I deeply thank anyone that attempts to help!
